一元二次方程
的解是
A． ， |
B． ， |
C． ， |
D．， |
在一张复印机复印出来的纸上，一个多边形图案的一条边由原来的1cm变成2cm，那么这次复印出来的多边形图案面积是原来的
| A．1倍 | B．2倍 | C．3倍 | D．4倍 |
把方程
配方化为
的形式是
A． |
B． |
C． |
D． |
下列命题中是假命题的是
| A．角平分线上的点到角两边的距离相等 | B．位似变换不改变图形的形状和大小 |
| C．等腰三角形两底角相等 | D．直角三角形斜边上的中线等于斜边的一半 |
下列两个图形一定相似的是
| A．任意两个等腰梯形 | B．任意两个菱形 | C．任意两个正方形 | D．任意两个矩形 |
的值等于
A． |
B． |
C． |
D． |
某班一些学生做图钉随机抛掷的实验，求图钉尖触地还是图钉面触地的概率，下列做法正确的是
| A．甲做了4000次，得出针尖触地的频率约为42%，于是他断定在做第4001次时，针尖肯定不会触地； |
| B．乙认为一次一次做，速度太慢，他拿来了大把材料，形状及大小都完全一样的图钉，随意朝上轻轻抛出，然后统计针尖触地的个数，这样大大提高了速度； |
| C．老师安排每位同学回家做实验，各人的图钉大小、质地均匀程度都不一样，同学交来的结果，老师进行统计； |
| D．老师安排同学回家做实验，图钉统一发（完全一样的图钉），同学交来的结果，老师进行统计。 |
已知两点
，
，且
，则点的C坐标为
A． |
B． |
C． |
D． |
方程
的根是 ．
把命题“分数一定是实数”改成“如果…那么…”
的形式是
如图，有6张牌，从中任意抽取一张，数字是奇数的概率是 
如图，为了测量学校旗杆的高度，小东用长为3.2m的竹竿做测量工具。移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为 m
已知，如图，一斜坡AB的坡度为
，则坡角
为 度
若
∽
，
，
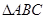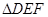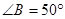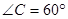，则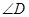
的度数为 ．
若关于
的一元二次方程
有两个相等的实数根，请你写出一组符合条件m、n的值，其中m= ，n=
某果农2008年的年收入为5万元，由于扩大了规模，2010年年收入增加到6.05万元，则平均每年的增长率是
计算：
解方程：
如图，在方格纸上，
与
是关于点O为位似中心的位似图形，他们的顶点都在格点上．
（1）画出位似中心O；
（2）求出与的位似比；
（3）以O点为位似中心，再画一个
使它与的位似比等于3
如图，在
中，若
，
，
，求BC的长.
为举为红色旅游节加强宣传力度，需要在甲楼A处至E处挂一幅宣传条幅。在乙楼顶部D点测得条幅顶端A点的仰角为
，条幅底端E点的俯角为
，若甲乙两楼之间的水平距离BC为21米，则条幅的长约为多少米？（
，
，结果精确到0.1米）
如图，A、B、C、D四张卡片上分别写有
，
，
，
四个实数，从中任取两张卡片．
（1）请列举出所有可能的结果（用字母A，B，C，D表示）
（2）求取到的两个数都是无理数的概率。
如图，在4×4的方格纸中，
和
的顶点都在格点上。
（1）填空：
度；
；
（2）判断与是否相似，请证明你的结论。
学校计划在一块长80m，宽60m的长方形场地的中央建一个长方形体育训练场地，场地面积为3500
．四周为宽度相等的人行走道，如图所示，求人行走道的宽度。
某场地有一堵旧墙，张强想利用这堵旧墙为一面，其余三面用100米长的篱笆材料围成一矩形露天仓库。
（1）若用该篱笆和旧墙围成一个面积为1200
的矩形，且旧墙长为50m，求矩形的长和宽；
（2）能用该篱笆和旧墙围成一个面积为1260的矩形吗？若能，请求出矩形的长和宽，若不能请说明理由。
（3）若用该篱笆和足够长的旧墙围成的矩形面积为m平方米，求m的取值范围。
如图所示 ，在等边中
，D、E分别是AB、AC上的点，
，如图（1），然后将
绕A点顺时针旋转
，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
（1）在图（2）中，线段BD与线段CE的大小关系是 ；
（2）在图（3）中，
与是相似三角形吗？请证明你的结论。