设集合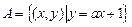 ,
,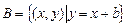 ,且
,且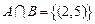 ,则( )
,则( )
A. |
B.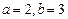 |
C.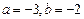 |
D.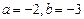 |
下列图像表示函数图像的是( )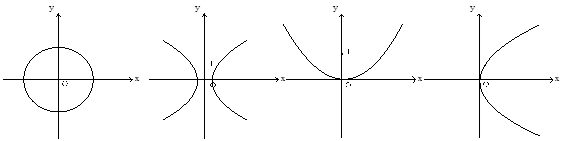
A B C D
函数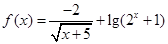 的定义域为( )
的定义域为( )
| A.(-5,+∞) | B.[-5,+∞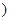 |
| C.(-5,0) | D.(-2,0) |
已知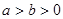 ,则
,则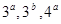 的大小关系是 ( )
的大小关系是 ( )
A.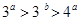 |
B.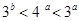 |
C.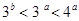 |
D.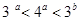 |
函数 的实数解落在的区间是( )
的实数解落在的区间是( )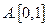
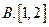

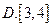
已知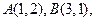 则线段
则线段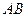 的垂直平分线的方程是 ( )
的垂直平分线的方程是 ( )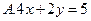
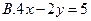
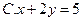
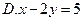
下列条件中,能判断两个平面平行的是 ( )
| A.一个平面内的一条直线平行于另一个平面; |
| B.一个平面内的两条直线平行于另一个平面 |
| C.一个平面内有无数条直线平行于另一个平面 |
| D.一个平面内任何一条直线都平行于另一个平面 |
在x轴上的截距为2且倾斜角为135°的直线方程为 ( )
A.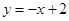 |
B.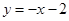 |
C. |
D.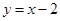 |
如果轴截面为正方形的圆柱的侧面积是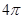 ,那么圆柱的体积等于( )
,那么圆柱的体积等于( )
A.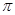 |
B.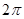 |
C.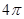 |
D.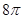 |
在圆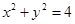 上,与直线
上,与直线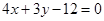 的距离最小的点的坐标为 ( )
的距离最小的点的坐标为 ( )
A.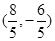 |
B.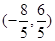 |
C.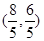 |
D.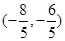 |
设点M是Z轴上一点,且点M到A(1,0,2)与点B(1,-3,1)的距离相等,则点M的坐标是:( )
| A.(-3,-3,0) | B.(0,0,-3) |
| C.(0,-3,-3) | D.(0,0,3) |
如图所示,阴影部分的面积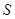 是
是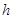
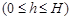 的函数.则该函数的图象是:( )
的函数.则该函数的图象是:( )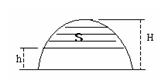
已知镭经过100年,质量便比原来减少4.24%,设质量为1
的镭经过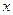 年后的剩留量为
年后的剩留量为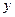 ,则
,则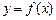 的函数解析式为 .
的函数解析式为 .
如果一个几何体的三视图如右图所示(单位长度:cm),
则此几何体的表面积是 .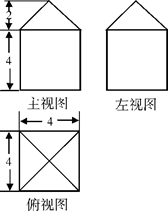
设函数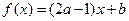 在R上是减函数,则
在R上是减函数,则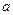 的范围是
的范围是
已知点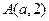 到直线
到直线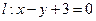 距离为
距离为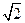 ,则
,则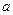 =
=
(本小题满分12分)
求经过两条直线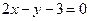 和
和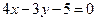 的交点,并且与直线
的交点,并且与直线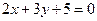 垂直的直线方程(一般式).
垂直的直线方程(一般式).
(本小题满分12分)
若非零函数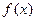 对任意实数
对任意实数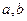 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当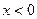 时,
时,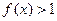 .
.
(1)求证: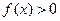
(2)求证: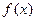 为减函数;
为减函数;
(3)当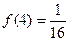 时,解不等式
时,解不等式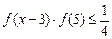
(本小题满分12分)
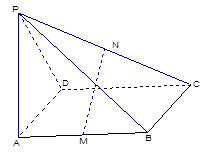
如图,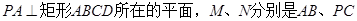 的中点.
的中点.
(1)求证: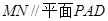 ;(2)求证:
;(2)求证: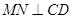 ;
; 
(本小题满分12分)
已知函数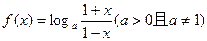
(1)求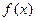 的定义域;
的定义域;
(2)判断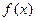 的奇偶性并证明;
的奇偶性并证明;
.(本小题满分12分)直线l经过点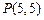 ,且和圆C:
,且和圆C: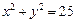 相交,截得弦长为
相交,截得弦长为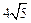 ,求l的方程.
,求l的方程.
(本小题满分14分)
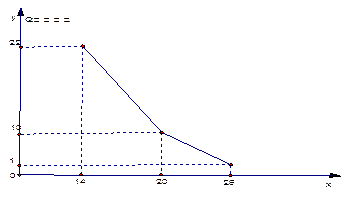
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如下图,每月各种开支2000元,
(1)写出月销售量Q(百件)与销售价格P(元)的函数关系。
(2)该店为了保证职工最低生活费开支3600元,问:商品价格应控制在什么范围?
(3)当商品价格每件为多少元时,月利润并扣除职工最低生活费的余额最大?并求出最大值。