下列图形中,表示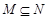 的是 ( )
的是 ( )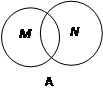
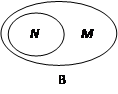
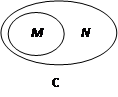
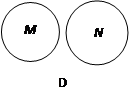
某扇形的圆心角为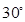 ,半径为2,那么该扇形弧长为 ( )
,半径为2,那么该扇形弧长为 ( )
A.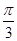 |
B.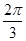 |
C.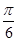 |
D.60 |
函数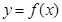 的图象与直线
的图象与直线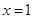 的公共点数目是( )
的公共点数目是( )
A.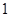 |
B.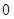 |
C.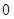 或 或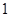 |
D.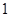 或 或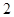 |
已知平面向量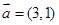 ,
, ,且
,且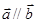 ,则
,则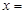 ( )
( )
A.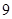 |
B.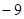 |
C.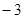 |
D.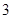 |
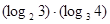 的值是( )
的值是( )
| A.2 | B.1 | C. |
D.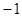 |
函数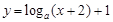 的图象过定点 ( )
的图象过定点 ( )
| A.(1,2) | B.(2,1) | C.(-2,1) | D.(-1,1) |
已知角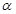 的终边经过点
的终边经过点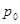 (-3,-4),则
(-3,-4),则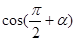 的值为( )
的值为( )
A.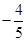 |
B. |
C. |
D.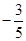 |
.要得到 的图象只需将y=3sin2x的图象( )
的图象只需将y=3sin2x的图象( )
A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移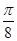 个单位 个单位 |
D.向右平移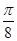 个单位 个单位 |
设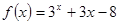 ,用二分法求方程
,用二分法求方程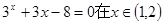 内近似解的过程中得
内近似解的过程中得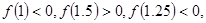 则方程的根落在区间( )
则方程的根落在区间( )
A.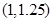 |
B.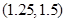 |
C.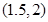 |
D.不能确定 |
已知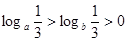 ,则下列关系正确的是( )
,则下列关系正确的是( )
A.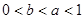 |
B.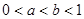 |
C.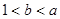 |
D.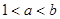 |
海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋. 如图:是某港口在某季节每天的时间与水深在直角坐标系中画出的散点图(时间为横坐标,水深为纵坐标)下列函数中,能近似描述这个港口的水深与时间的函数关系的是( )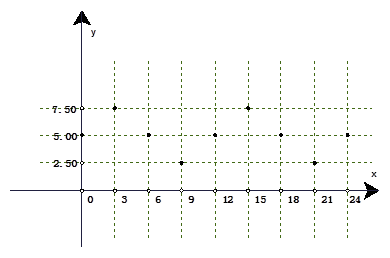
A.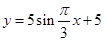 |
B.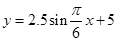 |
C.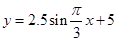 |
D.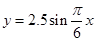 |
设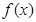 是定义在
是定义在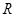 上的奇函数,且在区间
上的奇函数,且在区间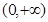 是单调递增,若
是单调递增,若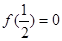 ,
, 的内角
的内角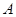 满足
满足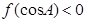 ,则
,则 的
的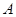 角取值范围是( )
角取值范围是( )
A.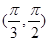 |
B.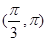 |
C.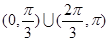 |
D.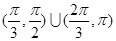 |
函数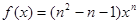 是幂函数,且在
是幂函数,且在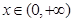 上是减函数,则实数
上是减函数,则实数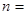 ______.
______.
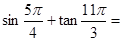 .
.
已知:两个函数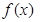 和
和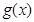 的定义域和值域都是
的定义域和值域都是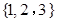 ,其定义如下表:
,其定义如下表:
| x |
1 |
2 |
3 |
|
x |
1 |
2 |
3 |
|
x |
1 |
2 |
3 |
| f(x) |
2 |
3 |
1 |
g(x) |
1 |
3 |
2 |
g[f(x)] |
|
|
|
填写后面表格,其三个数依次为: .
.对于下列命题:
①函数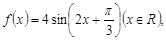
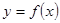 的图象关于点
的图象关于点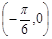 对称;
对称;
②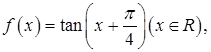 的单调增区间为
的单调增区间为
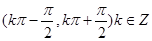 ;
;
③已知点N、P在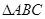 所在平面内,且
所在平面内,且 ,
,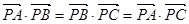 则N、P依次是
则N、P依次是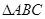 的重心、垂心;
的重心、垂心;
④已知向量 ,且
,且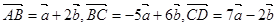 ,则三点
,则三点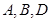 一定共线。以上命题成立的序号是__________________.
一定共线。以上命题成立的序号是__________________.
(本小题满分12分)(1)计算: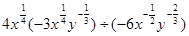 ;
;
(2)已知: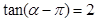 ,求:
,求: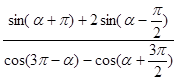 的值。
的值。
(本小题满分12分)在矩形ABCD中,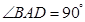
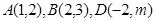 ;(1)求
;(1)求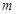 的值和点C的坐标?
的值和点C的坐标?
(2)求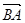 与
与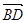 夹角
夹角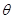 的余弦值;
的余弦值;
(本小题满分12分)已知函数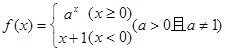 ;
;
(1)若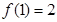 ,求
,求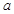 的值,并作出
的值,并作出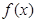 的图象;
的图象;
(2)当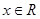 时,恒有
时,恒有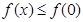 求
求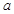 的取值范围。
的取值范围。
(本小题满分12分)大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数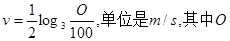 表示鱼的耗氧量的单位数,
表示鱼的耗氧量的单位数,
(1)当一条鱼的耗氧量是2700个单位时,它的游速是多少?
(2)计算一条鱼静止时耗氧量的单位数。
(本小题满分12分)函数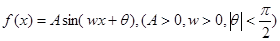 的一系列对应值如下表:
的一系列对应值如下表:
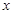 |
。。。 |
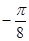 |
0 |
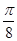 |
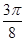 |
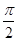 |
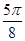 |
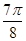 |
。。。 |
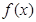 |
。。。 |
0 |
1 |
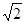 |
0 |
—1 |
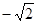 |
0 |
。。。 |
(1)根据表中数据求出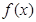 的解析式;
的解析式;
(2)指出函数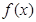 的图象是由函数
的图象是由函数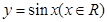 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;
(3)令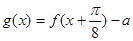 ,若
,若 在
在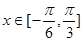 时有两个零点,求
时有两个零点,求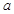 的取值范围。
的取值范围。
(本小题满分14分)已知函数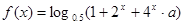 ;
;
(1)若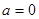 ,求
,求 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断 的单调性;(3)当
的单调性;(3)当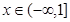 时
时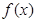 有意义求实
有意义求实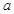 的范围。
的范围。