设集合 ,则
,则
A. |
B. |
C. |
D. |
“ 且
且 ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,下列命题中正确的是
是三个不同的平面,下列命题中正确的是
A. // // |
B. // // , , // //  // // |
C. // // |
D. // // , , // // // // |
由点 向直线
向直线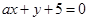 引垂线,垂足为
引垂线,垂足为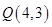 ,则
,则 的模为
的模为
A. |
B. |
C. |
D. |
已知向量 ,向量
,向量 与
与 的夹角为
的夹角为 ,且
,且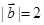 .则
.则
A. |
B.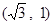 |
C. |
D. |
如右图,此程序框图的输出结果为
A. |
B. |
C. |
D. |

以双曲线的焦点为圆心,实轴长为半径的圆与双曲线的渐近线相切,则双曲线的离心率为
A.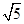 |
B. |
C. |
D. |
已知 且
且 ,则函数
,则函数 与函数
与函数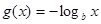 的图象可能是
的图象可能是
(A) (B) (C) (D)
若 满足不等式组
满足不等式组 则
则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
已知 函数
函数 是偶函数,则
是偶函数,则 的图象与
的图象与 轴交点纵坐标的最小值为
轴交点纵坐标的最小值为
A. |
B. |
C. |
D. |
学校为了调查学生在课外读物方面的支出情况,抽出高了一个 容量为 的样本,其频率分布直方图如图所示,其中.支出在
的样本,其频率分布直方图如图所示,其中.支出在 元的同学有
元的同学有 人,则
人,则 的值为
的值为

已知等差数列 中,
中, 则
则 
一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为 的圆,且这个几何体是球体的一部分,则这个几何体的表面积为 .
的圆,且这个几何体是球体的一部分,则这个几何体的表面积为 .
若 在椭圆
在椭圆 外 ,则过
外 ,则过 作椭圆的两条切线的切点为
作椭圆的两条切线的切点为 则切点弦
则切点弦 所在直线方程是
所在直线方程是 .那么对于双曲线则有如下命题: 若
.那么对于双曲线则有如下命题: 若 在双曲线
在双曲线
 外 ,则过
外 ,则过 作双曲线的两条切线的切点为
作双曲线的两条切线的切点为 则切点弦
则切点弦 的所在直线方程是
的所在直线方程是
已知向量 ,
, ,其中
,其中 ,则
,则 的夹角能成为直角三角形内角的概率是
的夹角能成为直角三角形内角的概率是
若定义在区间 上的函数
上的函数 对
对 上的任意
上的任意 个值
个值 ,
, ,…,
,…, ,总满足
,总满足 ≤
≤ ,则称
,则称 为
为 上的凸函数.已知函数
上的凸函数.已知函数 在区间
在区间 上是“凸函数”,则在
上是“凸函数”,则在 中,
中, 的最大值是___________
的最大值是___________
已知函数 在
在 上恒为增函数,则
上恒为增函数,则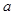 的取值范围是
的取值范围是
已知函数 ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.
(Ⅰ)求 的值及
的值及 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 求角
求角
已知 为平行四边形,
为平行四边形, ,
, ,
,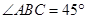 ,
, 是长方形,
是长方形, 是
是 的中点,
的中点, 平面
平面 平面
平面 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “
是 “ 类数列”.
类数列”.
(Ⅰ)已知数列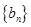 是 “
是 “ 类数列”且
类数列”且 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“ 类数列”,说明理由.
类数列”,说明理由.
已知函数 在
在 处取得极大值
处取得极大值 .
.
(Ⅰ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅱ)若过点 可作曲线
可作曲线 的切线有三条,求实数
的切线有三条,求实数 的取值范围.
的取值范围.
已知抛物线 的方程 为
的方程 为 ,直线
,直线 与抛物线
与抛物线 相交
相交
于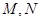 两点,点
两点,点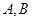 在抛物线
在抛物线 上.(Ⅰ)若
上.(Ⅰ)若 求证:直线
求证:直线
的斜率为定值;
(Ⅱ)若直线 的斜率为
的斜率为 且点
且点 到 直线
到 直线 的距离的和为
的距离的和为 ,试判断
,试判断 的形状,并证明你的结论.
的形状,并证明你的结论.