4 的平方根是( )
| A.2 | B.16 | C.±2 | D.±16 |
49的平方根为
| A.7 | B.-7 | C.±7 | D.± |
(-2)2的算术平方根是( )
| A.2 | B.±2 | C.-2 | D. |
16的算术平方根是 .
27的立方根为 ▲ .
(2011江苏南京,1,2分) 的值等于
的值等于
| A.3 | B.-3 | C.±3 | D. |
计算 的结果是
的结果是
A.±3 |
B.3 |
C.±3 | D.3 |
计算: = ____________.
下列各式中,正确的是( )
A. |
B. |
C. |
D. |
已知:一个正数的两个平方根分别是 和
和 ,则
,则 的值是 .
的值是 .
根式 中x的取值范围是( )
中x的取值范围是( )
A.x≥ |
B.x≤ |
C.x< |
D.x> |
若二次根式 有意义,则x的取值范围为( )
有意义,则x的取值范围为( )
A.x≥ |
B.x≤ |
C.x≥ |
D.x≤ |
(2011湖北黄冈,3,3分)要使式子 有意义,则a的取值范围为_____________________.
有意义,则a的取值范围为_____________________.
若等式 成立,则
成立,则 的取值范围是 .
的取值范围是 .
已知 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
(2011四川内江, 6分)已知 ,则
,则 .
.
若 ,则
,则 的值为 ( )
的值为 ( )
| A.1 | B.-1 | C.7 | D.-7 |
已知x,y为实数,且满足
 =0,那么x2011-y2011= .
=0,那么x2011-y2011= .
 则
则 =
=
下列运算正确的是( )
A. =±5 =±5 |
B. - - =1 =1 |
C. ÷ ÷ =9 =9 |
D. · · =6 =6 |
下列各式计算正确的是
A. |
B. |
C. |
D. |
下面计算正确的是( )
A. |
B. |
C. |
D. |
下列计算正确的是( )
A. |
B. |
C. |
D. |
计算2 -6
-6 +
+ 的结果是( )
的结果是( )
A.3 -2 -2 |
B.5- |
C.5- |
D.2 |
下列二次根式中,最简二次根式是( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
实数a在数轴上的位置如图所示,则 化简后为
化简后为
| A.7 | B.-7 | C.2a-15 | D.无法确定 |
如果 ,则( )
,则( )
A.a< |
B.a≤ |
C.a> |
D.a≥ |
已知 、
、 为两个连续的整数,且
为两个连续的整数,且 ,则
,则 .
.
设a=-1,a在两个相邻整数之间,则这两个整数是( )
| A.1和2 | B.2和3 | C.3和4 | D.4和5 |
在实数 、
、 、
、 、
、 中,最小的是( )
中,最小的是( )
A. |
B. |
C. |
D. |
(2011四川凉山州,25,5分)已知 为有理数,
为有理数, 分别表示
分别表示 的整数部分和小数部分,且
的整数部分和小数部分,且
 ,则
,则 。
。
化简: = ▲ .
= ▲ .
计算: = ▲ .
= ▲ .
化简: _____________.
_____________.
计算 .
.
计算 +
+ 之值为何?
之值为何?
A.5 |
B.3 |
C.3 |
D.9 |
17.计算 之值为何?
之值为何?
A. |
B. |
C. |
D. |
若 ,则
,则 的值是 .
的值是 .
已知 ,
, ,则代数式
,则代数式 的值为( )
的值为( )
| A.9 | B.±3 | C.3 | D.5 |
(2011山东德州12,4分)当 时,
时, =_____________.
=_____________.
(2011山东威海,13,3 分)计算
分)计算 的结果是 .
的结果是 .
计算 =_______________.
=_______________.
计算
对于任意不相等的两个实数a、b,定义运算※如下:a※b= ,如3※2=
,如3※2= .那么8※12= .
.那么8※12= .
计算: .
.
,4)计算:
,3分)化简:
计算:
先化简再计算: ,其中x是一元二次方程
,其中x是一元二次方程 的正数根.
的正数根.
化简,求值:  ) ,其中m=
) ,其中m= .
.
先化简,再求值:( )÷a,其中a=
)÷a,其中a= .
.
先化简,再求值:(a-1+ )÷(a2+1),其中a=
)÷(a2+1),其中a= -1.
-1.
(2011江苏泰州,20,8分)解方程组 ,并求
,并求 的值.
的值.
(2011四川成都,17,8分)先化简,再求值: ,其中
,其中 .
.
先化简,再求值: ,其中
,其中 .
.
(2011重庆綦江,21,10分) 先化简,再求值: 其中x=
其中x=
先化简,后求值:( )·(
)·( ),其中
),其中
(2011山东东营,18(2),4分)先化简,再求值:  ,其中
,其中
先化简再求值 其中a=
其中a=
(2011贵州安顺,20,8分)先化简,再求值: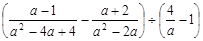 ,其中a=2-
,其中a=2-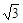
先化简,再求值: ,其中
,其中 .
.