（ 2011重庆江津， 2，4分）下列式子是分式的是( )
A． |
B． |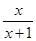
C． |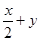
D． |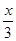
当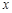
时，分式
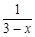有意义．
已知分式
，当
时，分式无意义，则
，当
时，使分式无意义的
的值共有 个．
当
= 时，分式
的值为零.
当8、分式
的值为0时，x的值是（ ）
| A．0 | B．1 | C．－1 | D．－2 |
如果分式
的值为0，则
的值应为 ．
已知
，则
的值是
A． |
B．－ |
C．2 | D．－2 |
设m＞n＞0，m2＋n2＝4mn，则
的值等于
A．2 |
B． |
C． |
D．3 |
若m为正实数，且
，
=
化简
的结果是（ ）
A． |
B． |
C． |
D．y |
计算：
的结果是（ ）
A． |
B． |
C． |
D． |
（2011浙江丽水，7，3分）计算 – 的结果为（ ）
| A． | B．－ | C．－1 | D．1－a |
（2011山东临沂，5，3分）化简（x－
）÷（1－
）的结果是（ ）
| A． |
B．x－1 | C． |
D． |
化简
的结果是
A． |
B． |
C． |
D．1 |
计算
的结果为（ ）
A． |
B．－ |
C．－1 | D． |
化简
的结果是 .
（2011山东泰安，22 ，3分）化简：（-）÷的结果为 。
化简：
＝__________________．
化简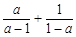
=________．
（2011江苏盐城，13，3分）化简： = ．
先化简，再求值：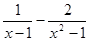
，其中x=－2．
,4分）（2）
先化简，再求值：
(
－2),其中x=2.
,4分）化简：
.
先化简，再求值：(－)÷，其中x满足x2－x－1＝0．
先化简，再求值
，其中
．
（2011湖南常德，19，6分）先化简，再求值.
已知
，求
的值。
（2011广东株洲，18，4分）当
时，求
的值．
，4分）
（（2011山东济宁，16，5分）计算：
先化简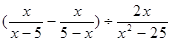
，然后从不等组
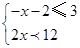的解集中，选取一个你认为符合题意的x的值代入求值．
（ 2011重庆江津， 21（3），6分）先化简,再求值: 
,其中
·
计算
在三个整式x2-1，x2+2x+1，x2+x中，请你从中任意选择两个，将其中一个作为分子，另一个作为分母组成一个分式，并将这个分式进行化简，再求当x=2时分式的值．
（2011广东肇庆，19，7分） 先化简，再求值：
，其中
．
化简:
（2011重庆市潼南,21,10分）先化简，再求值：
，其中a =
-1.
（2011山东枣庄，19，8分）先化简，再求值：÷，其中x＝－5．
先将代数式
化简，再从-1，1两数中选取一个适当的数作为
的值代入求值.
2011湖北武汉市，18，6分）先化简，再求值：
，其中x=3．
201１四川广元，17，7分）请先化简（
－
）÷
，再选取一个既使原式有意义，又是你喜欢的数代入求值．
计算
的结果是（ ）
A． |
B． |
C． |
D． |
2011内蒙古包头，17，3分）化简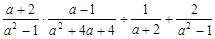
，其结果是 .