已知全集U={0,2,4,6,8,10},集合A={2,4,6}, B={10},则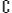 UA∪B为
UA∪B为
函数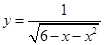 的定义域是
的定义域是
已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是
对于函数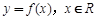 ,“
,“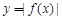 的图像关于
的图像关于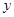 轴对称”是“
轴对称”是“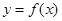 是奇函数”的 条件
是奇函数”的 条件
下列四个不等式:①a<0<b;②b<a<0;③b<0<a;④0<b<a,其中能使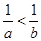 成立的充分条件有 (填序号)
成立的充分条件有 (填序号)
若函数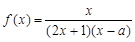 为奇函数,则
为奇函数,则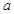 =
=
若不等式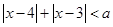 在
在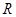 上的解集非空,则实数
上的解集非空,则实数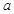 的取值范围是
的取值范围是
等差数列{an}中,Sn是其前n项和,a1=-11,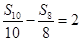 ,则S11=
,则S11=
若不等式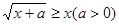 的解集为
的解集为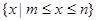 ,且
,且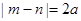 ,则a的取值集合为
,则a的取值集合为
已知集合A={x ||x+3|+|x-4|≤9,x∈R },B={x |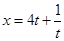 -6,t∈(0,+∞), x∈R },则集合A∩B=
-6,t∈(0,+∞), x∈R },则集合A∩B=
《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为____________升
已知函数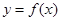 的定义域为
的定义域为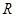 ,当
,当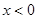 时,
时,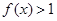 ,且对任意的
,且对任意的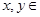
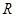 ,等式
,等式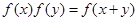 成立.若数列
成立.若数列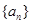 满足,
满足,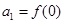
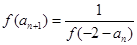
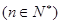
则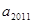 的值为
的值为
已知点O(0,0)、Q0(0,1)和点R0(3,1),记Q0R0的中点为P1,取Q0P1和P1R0中的一条,记其端点为Q1、R1,使之满足 ,记Q1R1的中点为P2,取Q1P2和P2R1中的一条,记其端点为Q2、R2,使之满足
,记Q1R1的中点为P2,取Q1P2和P2R1中的一条,记其端点为Q2、R2,使之满足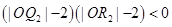 .依次下去,得到
.依次下去,得到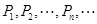 ,则
,则
若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ,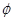 属于τ;
属于τ;
②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X ={a,b,c},对于下面给出的四个集合τ:
①τ={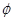 ,{a}, {c}, {a, b, c}}; ②τ={
,{a}, {c}, {a, b, c}}; ②τ={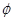 ,{b}, {c}, {b, c}, {a, b, c}};
,{b}, {c}, {b, c}, {a, b, c}};
③τ={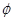 ,{a}, {a, b}, {a, c}}; ④τ={
,{a}, {a, b}, {a, c}}; ④τ={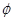 ,{a, c}, {b, c}, {c}, {a, b, c}}.
,{a, c}, {b, c}, {c}, {a, b, c}}.
其中是集合X上的拓扑的集合τ的序号是_________________
、设等差数列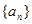 的前n项和为
的前n项和为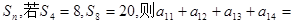 ()
()
| A.18 | B.17 | C.16 | D.15 |
设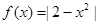 ,若
,若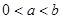 ,且
,且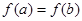 ,则
,则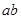 的取值范围是 ( )
的取值范围是 ( )
A.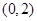 |
B.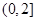 |
C.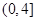 |
D.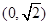 |
、已知函数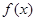 是
是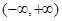 上的偶函数,若对于
上的偶函数,若对于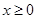 ,都有
,都有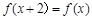 ,且当
,且当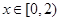 时,
时,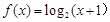 ,则
,则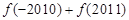 的值为 ( )
的值为 ( )
A.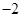 |
B.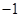 |
C.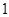 |
D.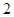 |
函数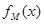 的定义域为R,且定义如下:
的定义域为R,且定义如下: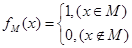 (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足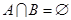 ,则函数
,则函数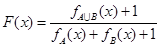 的值域为 ( )
的值域为 ( )
A.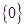
B.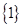
C.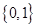
D.
已知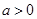 且
且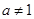 ,关于
,关于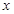 的不等式
的不等式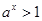 的解集是
的解集是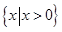 ,解关于
,解关于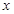 的不等式
的不等式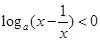
已知集合 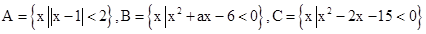
(1)若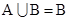 ,求
,求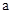 的取值范围
的取值范围
(2)若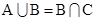 ,求
,求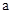 的取值范围
的取值范围
已知函数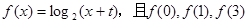 成等差数列,点
成等差数列,点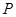 是函数
是函数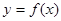 图像上任意一点,点
图像上任意一点,点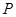 关于原点的对称点
关于原点的对称点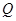 的轨迹是函数
的轨迹是函数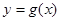 的图像
的图像
(1)解关于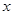 的不等式
的不等式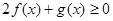
(2)当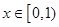 时,总有
时,总有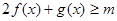 恒成立,求
恒成立,求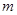 的取值范围
的取值范围
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%
(1) 求第n年初M的价值an的表达式
(2) 设An=,若An大于80万元,则M继续使用,否则须在第n年初对M更新.
问:该企业必须在第几年的年初对设备M更新?请说明理由
(1)等比数列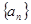 中,对任意
中,对任意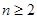 ,
,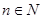 时都有
时都有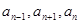 成等差,求公比
成等差,求公比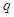 的值
的值
(2)设 是等比数列
是等比数列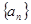 的前
的前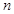 项和,当
项和,当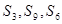 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由
(3)设等比数列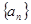 的公比为
的公比为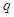 ,前
,前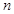 项和为
项和为 ,是否存在正整数
,是否存在正整数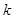 ,使
,使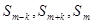 成等差且
成等差且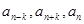 也成等差,若存在,求出
也成等差,若存在,求出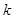 与
与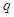 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由