设
，
，则下列不等式中一定成立的是
A． |
B． |
C． |
D． |
“
”是“
”的
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
x(x-3)(2-x)(x+1)>0的解集为（ ）
| A．（-1，1） | B． |
C． |
D． |
不等式
的解集是
，则
的值等于
| A．－14 | B．14 | C．－10 | D．10 |
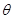在第二象限，
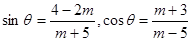，则
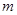满足
| A．m<-5或m>3 | B．3<m<9 | C．m=0或m=8 | D．m=0 |
不等式
的解集为
| A．（-1，1） | B． |
C． |
D． |
已知不等式
的解集是
，则
A． |
B． |
C． |
D． |
若
，
，则
与
的大小关系为
A． |
B． |
C． |
D．随x值变化而变化 |
下列函数中，最小值为4的是
A． |
B．  |
C． |
D．  |
如果
对任意实数x总成立,则a的取值范围是
A． |
B． |
C． |
D． |
图中阴影部分可用二元一次不等式组表示 
A． |
B． |
C． |
D． |
已知在（-1,1）上的奇函数f(x)是增函数，若
,则a的取值范围是
| A．（-1，1） | B．（0， ） |
C．（0，1） | D．（1，） |
若
，则
与
的大小关系是 ．
点
在直线x+2y=3上移动，则
的最小值是 .
某公司一年购买某种货物400吨，每次都购买
吨，运费为4万元/次，一年的总存储费用为
万元，要使一年的总运费与总存储费用之和最小，则
吨．
已知
, 则不等式
的解集___ _____．
已知集合
，
，求
解关于x的不等式
某学校校办工厂有毁坏的房屋一座，留有一面14m的旧墙，现准备利用这面墙的一段为面墙，建造平面图形为矩形且面积为126
的厂房（不管墙高），工程的造价是：
（1）修1m旧墙的费用是造1m新墙费用的25%;
（2）拆去1m旧墙用所得的材料来建1m新墙的费用是建1m新墙费用的50%.问如何利用旧墙才能使建墙的费用最低？
对任意
，函数
的值恒大于零，求
的取值范围．