设集合
，则（ ）
A．A B |
B．BA |
C．A |
D．B |
在复平面内，复数
对应的点位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
已知命题p：
，
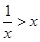，命题q ：
，
，则（ ）
A．命题 是假命题 |
B．命题 是真命题 |
C．命题 是假命题 |
D．命题 是真命题 |
预测人口的变化趋势有多种方法，“直接推算法”使用的公式是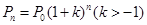
，其中Pn为预测人口数，P0为初期人口数，k为预测年内增长率，n为预测期间隔年数．如果在某一时期有-1<k<0，那么这期间人口数（ ）
| A．呈上升趋势 | B．呈下降趋势 |
| C．摆动变化 | D．不变 |
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）
A． |
B． |
C．1 | D．2 |
执行如右图所示的程序框图，输出的S值为（ ）
| A．650 | B．1250 | C．1352 | D．5000 |
．若函数
在区间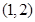
内有零点，则实数a的取值范围是（ ）
A． |
B． |
C． |
D． |
如图，P是正方体ABCD—A1B1C1D1对角线AC1上一动点，设AP的长度为x，若△PBD
的面积为f（x），则f（x）的图象大致是 （ ）
 （A） |
 （B） |
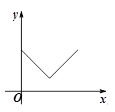 （C） |
 （D） |
过点（-1,3）且与直线x-2y+3=0平行的直线方程为 ．
已知函数
若
，则a=
．某个容量为100的样本的频率分布直方图如图所示，则数据在区间
上的频数是 ．
若向量
，
满足
，
，
，则向量与的夹角
等于___．
设Sn是等比数列{an}的前n项和，若S1，2S2，3S3成等差数列，则公比q等于 ．
函数
的导函数为
，若对于定义域内任意
，
，有
恒成立，则称为恒均变函数．给出下列函数：①
；②
；③
；④
；⑤
．其中为恒均变函数的序号是 ．（写出所有满足条件的函数序号）
（本小题共13分）已知函数
．
（Ⅰ）求函数
的最小正周期和值域；
（Ⅱ）若
为第二象限角，且
，求
的值．
（本小题共14分）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC，M，N分别是CC1，AB的中点．
（Ⅰ）求证：CN⊥AB1；
（Ⅱ）求证：CN //平面AB1M．
（本小题共13分）为了解某地区中学生的身体发育状况，拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查．已知甲、乙、丙三所中学分别有12，6，18个教学班．
（Ⅰ）求从甲、乙、丙三所中学中分别抽取的教学班的个数；
（Ⅱ）若从抽取的6个教学班中随机抽取2个进行调查结果的对比，求这2个教学班中至少有1个来自甲学校的概率．
（本小题共13分）在平面直角坐标系xOy中，
为坐标原点，以为圆心的圆与直线
相切．
（Ⅰ）求圆的方程；
（Ⅱ）直线
：
与圆交于
，
两点，在圆上是否存在一点
，使得四边形
为菱形，若存在，求出此时直线的斜率；若不存在，说明理由．
（本小题共14分）已知函数
．
（Ⅰ）若函数
在
，
处取得极值，求
，
的值；
（Ⅱ）若
，函数在
上是单调函数，求的取值范围．
．（本小题共13分）函数
的定义域为R，数列
满足
（
且
）．
（Ⅰ）若数列是等差数列，
，且
（k为非零常数， 且），求k的值；
（Ⅱ）若
，
，
，数列
的前n项和为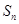
，对于给定的正整数
，如果
的值与n无关，求k的值．