已知集合 ,
,  ,
, , 则A
, 则A (
( IB)=
IB)=
A. |
B. |
C. |
D. |
已知 且
且 ,则“
,则“ ”是“
”是“ >1”的
>1”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
某路段200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为
| A.65辆 | B.76辆 | C.88辆 | D.95辆 |

如图表示一个几何体的三视图及相应数据,则该几何体的体积是
A. B.
B. C
C D.
D.

如图,已知 ,用
,用 表示
表示 ,则
,则
A. |
B. |
C. |
D. |

函数 的零点落在的区间是
的零点落在的区间是
A. |
B. |
C. |
D. |
在钝角△ABC中,已知AB= , AC=1,∠A=30°,则△ABC的面积是
, AC=1,∠A=30°,则△ABC的面积是
A. |
B. |
C. |
D. |
下列函数中,最小正周期为 ,且图象关于直线
,且图象关于直线 对称的是
对称的是
A. |
B. |
C. |
D. |
等差数列 项的和
项的和 等于
等于
A. |
B. |
C. |
D. |
两个正数a、b的等差中项是 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线
则双曲线 的离心率为
的离心率为
A. |
B. |
C. |
D. |
奇函数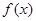 在区间
在区间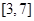 上是增函数,在区间
上是增函数,在区间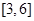 上的最大值为
上的最大值为 ,最小值为
,最小值为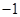 ,则
,则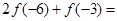 __________。
__________。
过原点且倾斜角为 的直线被圆
的直线被圆 所截得的弦长为__________
所截得的弦长为__________
如图,是一程序框图,则输出结果为 .
已知x>0,y>0且x+y=5,则lgx+lgy的最大值是
已知函数 .
.
(Ⅰ)若点 在角
在角 的终边上,求
的终边上,求 的值;
的值;
(Ⅱ)若 ,求
,求 的值域.
的值域.
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,若校医从“good sight”,中随机选取2人,试求抽到视力有5.2的学生的概率。
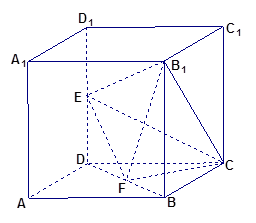
如图所示,在棱长为2的正方体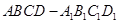 中,
中,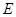 、
、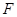 分别为
分别为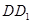 、
、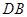 的中点.
的中点.
(Ⅰ)求证: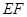 //平面
//平面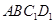 ;
;
(Ⅱ)求证: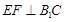 ;
;
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
 产品 产品消耗量 资源 |
甲产品(每吨) |
乙产品(每吨) |
资源限额(每天) |
| 煤(t) |
9 |
4 |
360 |
| 电力(kw·h) |
4 |
5 |
200 |
| 劳动力(个) |
3 |
10 |
300 |
| 利润(万元) |
6 |
12 |
|
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
已知抛物线 的焦点为F,椭圆C:
的焦点为F,椭圆C: 的离心率为
的离心率为 ,
, 是它们的一个交点,且
是它们的一个交点,且 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知 ,点A,B为椭圆
,点A,B为椭圆 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴, 是
是 的中点,试探究
的中点,试探究 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。
数列 ,且
,且 ,
, 为
为 的前
的前 项和.
项和.
(Ⅰ)求证:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(Ⅱ)如果对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.