下列根式中,是二次根式的是( )
A.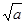 |
B.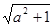 |
C.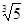 |
D. |
在函数 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
| A.x≥2 | B.x≥-2 | C.x≤-2 | D.x>2 |
、下列二次根式是最简二次根式的是( )
A. |
B.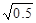 |
C. |
D.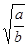 |
下列计算正确的是( )
A.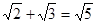 |
B. |
C.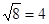 |
D. |
实数在数轴上对应点的位置如图所示,则化简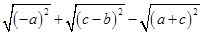 的结果为( )
的结果为( )
| A.-2a+b | B.2a-b+2c | C.b | D.-b |
关于x的方程(k-2) +3x-5=0是一元二次方程,则k的值为( )
+3x-5=0是一元二次方程,则k的值为( )
| A.±2 | B.2 | C.-2 | D.±1 |
一元二次方程x2+3x+4=0的根的情况是( )
A.有两个不相等的实数根 |
B.有两个相等的实数根 |
C.有两个实数根 |
D.没有实数根 |
用换元法解方程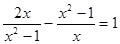 ,如果设
,如果设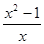 =y,则原方程可变形为( )
=y,则原方程可变形为( )
| A.2y2 -y-1="0" | B.2y2 +y-1=0 | C.y2 –y+2=0 | D.y2 +y-2=0 |
一元二次方程x2=4x的根是( )
| A.4 | B.±2 | C.0或2 | D.0或4 |
如图,小正方形的边长均为1,则图中三角形(粗线)与左图中△ABC相似的是( )
如图,在梯形ABCD中,AD∥BC,中位线EF与对角线BD交于点G。若EG﹕GF=2﹕3,且AD=8,则BC的长是( )
| A.12 | B.24 | C.6 | D.16 |

如图,给出下列条件:① ;②
;② ;③
;③ ;
;
④ 其中单独能够判定
其中单独能够判定 的个数为( )
的个数为( )
| A.1 | B.2 | C.3 | D.4 |

比较二次根式的大小:

计算: =
=
关于x的一元二次方程kx2-2x+1=0有两个实数根,
则k的取值范围是
关于x的方程x2-kx+2=0的一个根是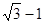 ,则另一根是__ _,k=___
,则另一根是__ _,k=___
已知 ,则x的取值范围是
,则x的取值范围是
若最简二次根式 和
和 是同类二次根式,那么a= ;b=
是同类二次根式,那么a= ;b=
若DE是△ABC的中位线, 3,则
3,则 ___
___
如图所示,已知点 分别是
分别是 中
中 边的中点,
边的中点,
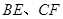 相交于点
相交于点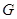 ,
, ,则
,则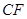 的长为
的长为 
计算:
解方程:x2-x-3=0
解方程: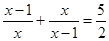
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)画出图形。
写出B、C两点的对应点B'、C'的坐标;如果△OBC内部一
 点M的坐标为(x,y),写出M的对应点M'的坐标。
点M的坐标为(x,y),写出M的对应点M'的坐标。
如图,在△ABC中,∠C=90°,D、E分别为AB、AC边上的两点,且AD·AB=AE·AC,求证:DE⊥AB.
某超市每年的营业额在不断的增长,2008年营业额是100万元,2010年营业额达到144万元。求2009年、20
 10年营业额的年平均增长率是多少?
10年营业额的年平均增长率是多少?若2011年营业额继续稳步增长(即年增长率与前两年的增长率相同),那么请你估计2011年营业额将达到多少万元?
如图:靠着22 m的房屋后墙,围一块150 m2的矩形鸡场,现在有篱笆共40 m。求
 矩形的长、宽各多少米?
矩形的长、宽各多少米?若把“围一块150 m
 2的矩形鸡场”改为“围一块Sm2的矩形鸡场”其它条件不变,能否使S最大。若能,请你求出此时矩形的长、宽及最大面积;若不能,请你说明理由。
2的矩形鸡场”改为“围一块Sm2的矩形鸡场”其它条件不变,能否使S最大。若能,请你求出此时矩形的长、宽及最大面积;若不能,请你说明理由。
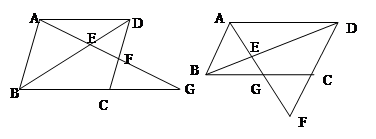
在□ABCD中,G为BC延长线上一点,射线AG与直线BD相交于E、与直线CD相交于F.求证:
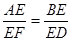 ;
;求证:AE2=E
 F●EG;
F●EG;如果把“G为BC延长线上一点”改为“G为线段BC上一点(不与点B、C重合)”,其它条件不变,(2)中的结论是否成立吗?若成立,请你加以证明;若不成立,请你说明理由。