已知集合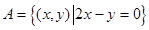 ,
,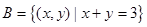 ,则
,则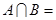 ( )
( )
A. |
B. |
C.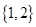 |
D. |
已知某校高一学生的学号后三位数字从001编至818,教育部门抽查了该校高一学生学号后两位数字是16的同学的体育达标情况.这里所用的抽样方法是 ( )
| A.抽签法 | B.分层抽样 | C.系统抽样 | D.随机数表法 |
集合M={ |
| }与N={
}与N={ |
| }之间的关系是( )
}之间的关系是( )
A.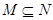 |
B.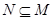 |
C. |
D. |
如果执行右面的程序框图,那么输出的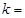 ( )
( )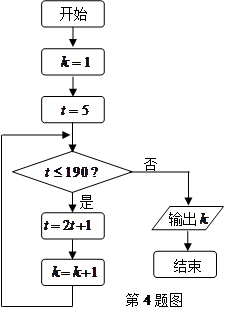
A. |
B. |
C.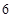 |
D.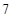 |
从装有5个红球和2个黑球的口袋中任取3个球,那么互斥而不对立的两个事件是( )
| A.至少有1个黑球与都是红球 |
| B.恰有1个黑球与恰有2个黑球 |
| C.至少有1个黑球与至少有1个红球 |
| D.至少有1个黑球与至少有2个红球 |
已知A,B,C是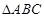 的三个内角,则下列各式中化简结果一定是0的是( )
的三个内角,则下列各式中化简结果一定是0的是( )
A. |
B.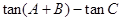 |
C. |
D. |
.已知函数 在
在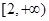 是增函数,则实数
是增函数,则实数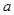 的取值范围是( )
的取值范围是( )
A. |
B. |
C.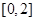 |
D.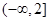 |
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量Pmg/L与时间t h间的关系为 .若在前5个小时消除了
.若在前5个小时消除了 的污染物,则污染物减少
的污染物,则污染物减少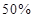 所需要的时间约为( )小时. (已知lg2=0.3010,lg3=0.4771)
所需要的时间约为( )小时. (已知lg2=0.3010,lg3=0.4771)
| A.26 | B.33 | C.36 | D.42 |
已知函数 ,
, R.则对任意实数
R.则对任意实数 ,函数
,函数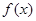 不可能( )
不可能( )
| A.是奇函数 | B.既是奇函数,又是偶函数 |
| C.是偶函数 | D.既不是奇函数,又不是偶函数 |
已知函数 与函数
与函数 有一个相同的零点,则
有一个相同的零点,则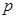 与
与 ( )
( )
| A.均为正值 | B.均为负值 | C.一正一负 | D.至少有一个等于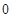 |
已知A,B是对立事件,若 ,则
,则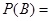 .
.
若 ,则与
,则与 具有相同终边的最小正角为 .
具有相同终边的最小正角为 .
在半径为10米的圆形弯道中,120°角所对应的弯道长为 米.
化简 = .
= .
函数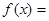
 的值域
的值域
已知 ,则函数
,则函数 ,
, R的最大值
R的最大值 = .
= .
已知函数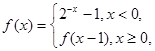 则满足
则满足 的实数
的实数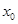 的集合是 .
的集合是 .
.
设集合 ,
, .
.
(1)求 ;
;
(2)若集合 满足
满足 ,求
,求 的取值范围.
的取值范围.
(本题满分7分)
已知 是第三象限角,且
是第三象限角,且 .
.
(1)求 的值;
的值;
(2)设 的终边与单位圆交于点
的终边与单位圆交于点 ,求点
,求点 的坐标.
的坐标.
(本题满分8分)
爱因斯坦提出:“人的差异在于业余时间”.某校要对本校高一学生的周末学习时间进行调查.现从中抽取50个样本进行分析,其频率分布直方图如图所示.记第一组[0,2),第二组[2,4),…,以此类推.
(1)根据频率分布直方图,估计高一段学生周末学习的平均时间;
(2)为了了解学习时间较少同学的情况,现从第一组、第二组中随机抽取2位同学,问恰有一位同学来自第一组的概率.
本题满分10分)
已知函数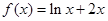
(1)判断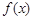 的单调性并用定义证明;
的单调性并用定义证明;
(2)设 ,若对任意
,若对任意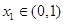 ,存在
,存在 (
(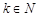 ),使
),使 ,求实数
,求实数 的最大值.
的最大值.