设集合
,则
（ ）
A． |
B． |
C． |
D． |
复数
满足
,其中
为虚数单位,则在复平面上复数对应的点位（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
某学校有教师150人，其中高级教师15人，中级教师45人，初级教师90人. 现按职称分层抽样选出30名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为（ ）
A． |
B．3,9,18 | C．3,10,17 | D．5,9,16 |
是
的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知实数4，
，9构成一个等比数列，则圆锥曲线
的离心率为（ ）
A． |
B． |
C． |
D． |
．设
是不同的直线， 
是不同的平面,下列四个命题中，正确的是（ ）
A．若 ,则 |
B．若 则 |
C．若 则 |
D．若 则 |
函数
的部分图象如图所示，那么
（ ）
A． |
B． |
C． |
D． |
.先后掷两次正方体骰子（骰子的六个面分别标有点数1、2、3、4、5、6），骰子朝上的面的点数分别为
，则
是奇数的概率是（ ）
A． |
B． |
C． |
D． |
在边长为6的正
中，点
满足
则
等于（ ）
| A．6 | B．12 | C．18 | D．24 |
设集合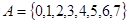
，如果方程
至少有一个根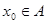
，就称方程为合格方程，则合格方程的个数为（ ）
| A．13 | B．15 | C．17 | D．19 |
一个几何体的三视图及其尺寸(单位：cm) ，如右图所示，则该几何体的侧面积为 cm
已知
满足条件
，则
的最大值为
某程序的框图如图所示，若执行该程序，则输出的
值为 
已知点
在直线
上，则
的最小值为 .
已知圆
过点
的直线
将圆
分成弧长之比为
的两段圆弧，则直线的方程为 .
.对于正项数列
，定义
,若
则数列
的通项公式为 .
在直角坐标系中,
的两个顶点
坐标分别为
,平面内两点
同时满足下列条件:
则的另一个顶点
的轨迹方程为
已知向量
与
共线，且有函数
（Ⅰ）求函数的周期与最大值；
（Ⅱ）已知锐角DABC的三个内角分别是A、B、C，若有
，边
，
，求AC的长.
已知正项数列
的前项和为
，且满足
（1）求数列的通项公式；（2）设
，则是否存在数列
，满足
对一切正整数
都成立？若存在，请求出数列的通项公式；若不存在，请说明理由.
如图，在直三棱柱
中，
，点
是
的中点。
（1）证明：平面
平面
；
（2）求
与平面
所成角的正切值；
已知函数
其中
是常数.
（1）当
时，求
在点
处的切线方程；
（2）求在区间
上的最小值.
如图，已知动直线
经过点
，交抛物线
于
两点，坐标原点
是
的中点，设直线
的斜率分别为
.
（1）证明：
（2）当
时，是否存在垂直于
轴的直线
，被以
为直径的圆截得的弦长为定值？若存在，请求出直线的方程；若不存在，请说明理由.