命题“ ”的否定是 。
”的否定是 。
已知集合 ,若
,若 ,则实数a的取值范围是 。
,则实数a的取值范围是 。
已知 ,若向量
,若向量 平行,则实数k= 。
平行,则实数k= 。
双曲线 的渐近线方程为 。
的渐近线方程为 。
如图,在棱长为2的正方体ABCD—A1B1C1D1中,E,F
分别是棱AB,BC中点,则三棱锥B—B1EF的体积为 。
在等比数列 中,若
中,若 ,则
,则 = .
= .
已知在等差数列 中,满足
中,满足 ,则该数列前n项和
,则该数列前n项和 的最小值是 .
的最小值是 .
在平面直角坐标系 中,点P在曲线
中,点P在曲线 上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 。
上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 。
已知 ,则β= 。
,则β= 。
.已知函数 在区间
在区间 上恒有
上恒有 ,则实数
,则实数 的取值范围是 。
的取值范围是 。
已知定义在R上的奇函数 满足
满足 时,
时, ,若
,若 ,则
,则 = 。
= 。
已知 ,函数
,函数 的最大值为
的最大值为 ,则实数
,则实数 的值为 .
的值为 .
给出下列五个命题:①当 时,有
时,有 ;②
;② 中,
中, 是
是 成立的充分必要条件;③函数
成立的充分必要条件;③函数 的图像可以由函数
的图像可以由函数 (其中
(其中 )的图像通过平移得到;④已知
)的图像通过平移得到;④已知 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则
,则 ;⑤函数
;⑤函数 与函数
与函数 的图像关于直线
的图像关于直线 对称。其中正确命题的序号为 。
对称。其中正确命题的序号为 。
设二次函数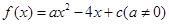 的值域为
的值域为 ,且
,且 ,则
,则 的最大值是 。
的最大值是 。
已知集合 函数
函数 的定义域为集合B。
的定义域为集合B。
(I)若 ,求集合
,求集合 ;
;
(II)已知 是“
是“ ”的必要条件,求实数a的取值范围。
”的必要条件,求实数a的取值范围。
已知函数
(I)求 的最大值和最小正周期;
的最大值和最小正周期;
(II)若 ,求
,求 的值。
的值。
定义在R上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
(I)试求 的值并证明函数
的值并证明函数 为奇函数;
为奇函数;
(II)若 对任意
对任意 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
如图为河岸一段的示意图,一游泳者站在河岸的A点处,欲前往河对岸的C点处。若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C。已知此人步行速度为v,游泳速度为0.5v。
(I)设 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为 的函数;并求自变量
的函数;并求自变量 取值范围;
取值范围;
II)当 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
已知函数
(I)当a=2时,求函数 的最大值和最小值;
的最大值和最小值;
(II)若函数 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(III)当a=1时,求证:
.
已知等差数列 的首项为
的首项为 ,公差为b,等比数列
,公差为b,等比数列 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。
(I)若 ,求数列
,求数列 的通项公式;
的通项公式;
(II)对于(1)中的数列 ,对任意
,对任意 在
在 之间插入
之间插入 个2,得到一个新的数列
个2,得到一个新的数列 ,试求满足等式
,试求满足等式 的所有正整数m的值;
的所有正整数m的值;
(III)已知 ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。