已知集合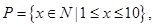 集合
集合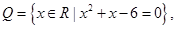 则
则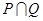 等于
等于
A.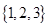 |
B.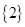 |
C. |
D.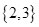 |
已知直线 ∥平面
∥平面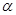 ,
,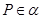 ,那么过点
,那么过点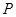 且平行于直线
且平行于直线 的直线( )
的直线( )
A.只有一条,不在平面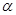 内 内 |
B.有无数条,不一定在平面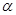 内 内 |
C.只有一条,且在平面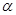 内 内 |
D.有无数条,一定在平面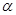 内. 内. |
已知函数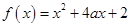 在区间
在区间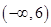 内单调递减,则a的取值范围是
内单调递减,则a的取值范围是
A.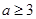 |
B.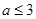 |
C.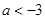 |
D.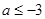 |
设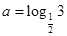 ,
,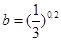 ,
,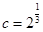 ,则
,则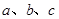 的大小顺序为
的大小顺序为
A.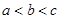 |
B.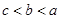 |
C.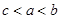 |
D.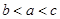 |
一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是
A.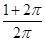 |
B.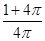 |
C.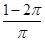 |
D.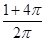 |
在同一坐标系中,函数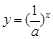 与
与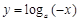 (其中
(其中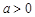 且
且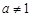 )的图象只可能是
)的图象只可能是
已知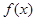 是奇函数,且方程
是奇函数,且方程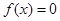 有且仅有3个实根
有且仅有3个实根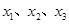 ,则
,则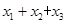 的值为
的值为
| A.0 | B.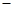 1 1 |
C.1 | D.无法确定 |
如图是正方体的平面展开图,在这个正方体中;⑴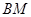 与
与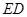 平行;⑵
平行;⑵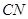 与
与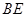 是异面直线;
是异面直线;
⑶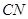 与
与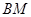 成
成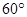 ;⑷
;⑷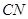 与
与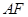 垂直. 以上四个命题中,正确命题的序号是( )
垂直. 以上四个命题中,正确命题的序号是( )
| A.⑴⑵⑶ | B.⑵⑷ | C.⑶ | D.⑶⑷ |
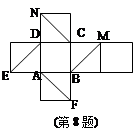
函数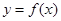 是R上的偶函数,且在
是R上的偶函数,且在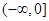 上是增函数,若
上是增函数,若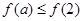 ,则实数
,则实数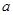 的取值范围是
的取值范围是
A.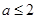 |
B.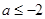 或 或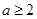 |
C.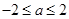 |
D.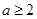 |
方程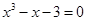 的实数解所在的区间是
的实数解所在的区间是
A.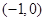 |
B.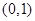 |
C.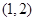 |
D.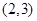 |
函数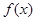 定义域为R,且对任意
定义域为R,且对任意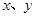
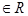 ,
,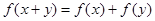 恒成立.则下列选项中不恒成立的是
恒成立.则下列选项中不恒成立的是
A.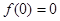 |
B.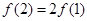 |
C.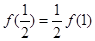 |
D.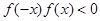 |
函数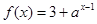 (
( )的图像总是经过定点______
)的图像总是经过定点______
将函数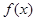
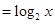 的图像水平向左平移1个单位,再关于
的图像水平向左平移1个单位,再关于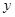 轴对称,得到函数
轴对称,得到函数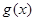 的图像,则
的图像,则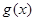 的函数解析式为
的函数解析式为
右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 . 
给出封闭函数的定义:若对于定义域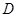 内的任意一个自变量
内的任意一个自变量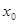 ,都有函数值
,都有函数值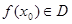 ,则称函数
,则称函数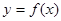 在
在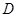 上封闭。若定义域
上封闭。若定义域 ,则函数①
,则函数①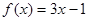 ;②
;②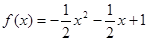 ;③
;③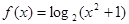 ;④
;④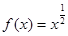 ,其中在
,其中在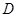 上封闭的是 .
上封闭的是 .
(填序号即可)
计算下列各式的值:
(1)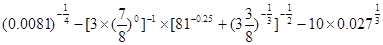 ;
;
(2) 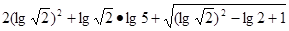 ;
;
设集合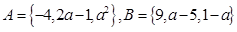 ,若
,若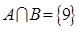 ,求实数
,求实数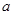 的值.
的值.
某公司打算在甲、乙两地促销同一种汽车,已知两地的销售利润(单位:万元)与销售量(单位:辆)之间的关系分别为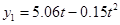 和
和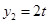 ,其中
,其中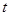 为销售量(
为销售量(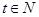 )。公司计划在这两地共销售15辆汽车。
)。公司计划在这两地共销售15辆汽车。
(1)设甲地销售量为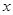 ,试写出公司能获得的总利润
,试写出公司能获得的总利润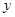 与
与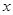 之间的函数关系;
之间的函数关系;
(2)求公司能获得的最大利润。
已知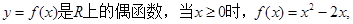
①求当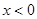 时,
时, 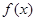 的解析式;
的解析式;
②作出函数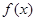 的图象,并指出其单调区间。
的图象,并指出其单调区间。
已知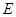 、
、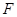 、
、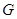 、
、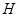 分别是正方体
分别是正方体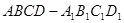 的棱
的棱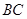 、
、 、
、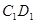 、
、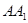 的中点。
的中点。
求证:①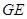 ∥平面
∥平面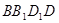 ;
;
②平面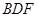 ∥平面
∥平面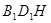
在正方体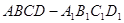 中,
中, 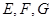 是
是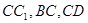 的中点
的中点
求证:①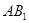 ∥平面
∥平面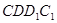 ;
;
②平面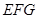 ∥平面
∥平面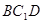
已知函数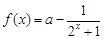 .
.
(1)求证:不论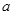 为何实数,
为何实数,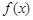 总为增函数;
总为增函数;
(2)求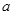 的值,使
的值,使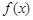 为奇函数;
为奇函数;
(3)当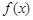 为奇函数时,求
为奇函数时,求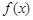 的值域。
的值域。
用定义证明:函数 在(0,1]上是减函数。
在(0,1]上是减函数。
设函数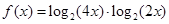 ,
,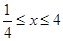 ,
,
(1)若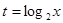 ,求
,求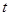 取值范围;
取值范围;
(2)求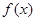 的最值,并给出最值时对应的x的值。
的最值,并给出最值时对应的x的值。
已知函数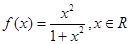 .
.
(1)求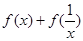 的值;
的值;
(2)计算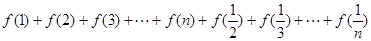 的值.
的值.