命题“若 ,则
,则 ”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )
”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )
| A.0 | B.2 | C.3 | D.4 |
“ ”是方程“
”是方程“ 表示双曲线”的( )
表示双曲线”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.都不是 |
已知命题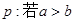 ,则
,则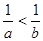 ,那么“
,那么“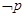 ”是( )
”是( )
A.若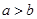 ,则 ,则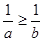 |
B.若 ,则不一定有 ,则不一定有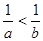 |
C.若 ,则 ,则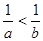 |
D.若 ,则 ,则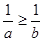 |
若双曲线 的离心率为2,则双曲线的渐近线方程为( )
的离心率为2,则双曲线的渐近线方程为( )
A. |
B. |
C. |
D. |
若双曲线 和椭圆
和椭圆 的离心率互为倒数,则以
的离心率互为倒数,则以 、
、 、
、 为边长的三角形是( )
为边长的三角形是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等腰三角形 |
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且∠
为椭圆上一点,且∠ ,则Δ
,则Δ 的面积为( )
的面积为( )
A. |
B. |
C. |
D. |
设 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段 中点
中点 的轨迹方程是( )
的轨迹方程是( )
A. |
B. |
C. |
D. |
若函数 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数 的图象是( )
的图象是( )
落在平静水面上的石头,使水面产生同心圆形波纹,在持续的一段时间内,若最外一圈的半径 (单位:米)与时间
(单位:米)与时间 (单位:秒)的函数关系是
(单位:秒)的函数关系是 ,则在2秒末扰动水面面积的变化率为( )
,则在2秒末扰动水面面积的变化率为( )
A. |
B. |
C. |
D. |
已知函数 ,则
,则 的图象在与
的图象在与 轴交点处的切线与两坐标轴围成的图形的面积为( )
轴交点处的切线与两坐标轴围成的图形的面积为( )
| A.1 | B. |
C. |
D. |
命题“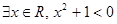 ”的否定是 .
”的否定是 .
用“充分、必要、充要”填空:
(1) 为真命题是
为真命题是 为真命题的 条件;
为真命题的 条件;
(2) 为假命题是
为假命题是 为真命题的 条件;
为真命题的 条件;
椭圆 的离心率为
的离心率为 ,则
,则 的值为 。
的值为 。
若直线 与双曲线
与双曲线 始终有公共点,则
始终有公共点,则 取值范围是 。
取值范围是 。
抛物线形拱桥,当水面离拱顶2米时,水面宽4米,若水面下降1米,则水面宽度为 米。
若对于任意的 ,有
,有 ,则此函数解析式为 。
,则此函数解析式为 。
下列关于圆锥曲线的命题:
① 设A,B为两个定点,若 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
② 设A,B为两个定点,若动点P满足 ,且
,且 ,则
,则 的最大值为8;
的最大值为8;
③ 方程 的两根可分别作椭圆和双曲线的离心率;
的两根可分别作椭圆和双曲线的离心率;
④ 双曲线 与椭圆
与椭圆
 有相同的焦点。
有相同的焦点。
其中真命题的序号 (写出所有真命题的序号)。
已知命题p:方程 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。
平面内与两定点 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为 ,它与直线
,它与直线 相交于P、Q两点,若
相交于P、Q两点,若 ,求椭圆方程。
,求椭圆方程。
已知直线 为曲线
为曲线 在点
在点 处的切线,直线
处的切线,直线 是该曲线的另一条切线,且
是该曲线的另一条切线,且 。
。
(1)求直线 和
和 的方程。
的方程。
(2)求直线 、
、 与x轴围成的三角形的面积。
与x轴围成的三角形的面积。
设点 为平面直角坐标系
为平面直角坐标系 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点 的距离比点P到
的距离比点P到 轴的距离大
轴的距离大 。
。
(1)求点P的轨迹方程。
(2)若直线 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且 ,求
,求 的值。
的值。
(3)设点P的轨迹是曲线C,点 是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
是曲线C上的一点,求以Q为切点的曲线C 的切线方程。