已知集合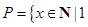 ≤
≤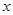 ≤
≤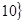 ,集合
,集合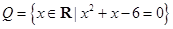 ,则
,则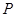 ∩
∩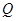 等于
等于
| A.{2} | B.{3} | C.{-2,3} | D.{-3,2} |
已知幂函数 的图象过点(
的图象过点( ,
, ),则
),则 的值是
的值是
A. |
B.1 | C.2 | D.4 |
某扇形的半径为 ,它的弧长为
,它的弧长为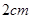 ,那么该扇形圆心角为
,那么该扇形圆心角为
| A.2° | B.2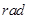 |
C.4° | D.4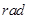 |
某商品降价 后,欲恢复原价,需再提价
后,欲恢复原价,需再提价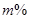 ,则
,则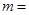
| A.10 | B.9 | C.11 | D.11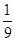 |
函数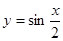 是
是
A.周期为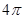 的奇函数 的奇函数 |
B.周期为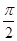 的奇函数 的奇函数 |
C.周期为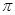 的偶函数 的偶函数 |
D.周期为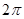 的偶函数 的偶函数 |
已知定义在R上的奇函数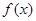 满足
满足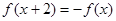 ,则
,则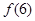 的值为
的值为
| A.-1 | B.0 | C.1 | D.2 |
已知平面向量a=(1,2),b=(-2,m)且a∥b,则2a+3b=
| A.(-5,-10) | B.(-4,-8) | C.(-3,-6) | D.(-2,-4) |
已知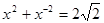 ,且
,且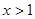 ,则
,则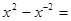
| A.2或-2 | B.-2 | C.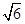 |
D.2 |
设函数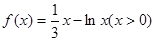 ,则
,则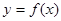
A.在区间(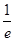 , ,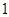 )、( )、(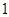 , ,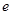 )内均有零点 )内均有零点 |
B.在区间(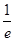 , ,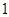 )、( )、(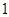 , ,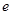 )内均无零点 )内均无零点 |
C.在区间(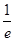 , ,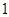 )内有零点,在区间( )内有零点,在区间(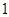 , ,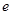 )内无零点 )内无零点 |
D.在区间(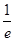 , ,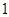 )内无零点,在区间( )内无零点,在区间(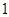 , ,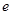 )内有零点 )内有零点 |
函数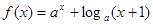 在
在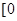 ,
,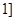 上的最大值与最小值之和为a,则a的值为
上的最大值与最小值之和为a,则a的值为
A.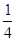 |
B. |
C.2 | D.4 |
将函数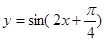 的图象向右平移
的图象向右平移 个单位,再把所得图象上各点横坐标缩小到原来的
个单位,再把所得图象上各点横坐标缩小到原来的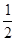 ,则所得函数解析式为
,则所得函数解析式为
A. |
B.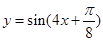 |
C.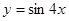 |
D.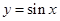 |
若函数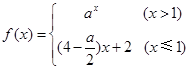 是R上的增函数,则实数a的取值范围为
是R上的增函数,则实数a的取值范围为
A.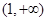 |
B.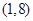 |
C.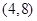 |
D.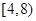 |
若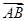 =2e1+e2,
=2e1+e2,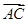 =e1-3e2,
=e1-3e2,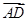 =5e1+λe2,且B、C、D三点共线,则实数λ=__________.
=5e1+λe2,且B、C、D三点共线,则实数λ=__________.
设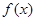 是定义在R上的奇函数,且x>0时,
是定义在R上的奇函数,且x>0时,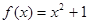 ,则当
,则当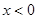 时,
时,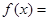 __________.
__________.
函数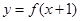 的定义域是[0,2],且
的定义域是[0,2],且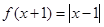 ,则
,则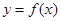 的单调递减区间是__________.
的单调递减区间是__________.
函数y=2sin(ωx+φ)( ,
, )的部分图
)的部分图
象如图所示,则ω和φ的值分别是__________.
已知全集U=R,集合M={x|x≤a-2或x≥a+3},N={x|-1≤x≤2}.
(1)若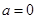 ,求(
,求(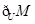 )∩(
)∩(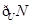 );
);
(2)若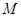 ∩
∩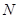 =
=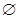 ,求实数
,求实数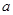 的取值范围.
的取值范围.
已知|a|=4,|b|=3,(2a-3b) (2a+b)=61.
(2a+b)=61.
(1)求a与b的夹角;
(2)求|a+b|与|a-b|.
正在建设中的长春地铁一号线将大大缓解市内南北交通的压力. 根据测算,如果一列车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次;每天来回次数是每次拖挂车厢节数的一次函数,每节车厢单向一次最多能载客110人,试问每次应拖挂多少节车厢才能使该列车每天营运人数最多?并求出每天最多的营运人数.(注:营运人数指列车运送的人数) .
已知向量a=
 ,b=
,b= ,c=
,c= ,
,
(1)求证:(a+b)⊥(a-b);
(2)设函数
 ,求
,求 的最大值和最小值.[来
的最大值和最小值.[来
定义在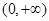 上的函数
上的函数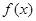 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有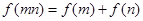 成立,当x>1时,
成立,当x>1时,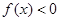 .
.
(1)求证:1是函数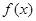 的零点;
的零点;
(2)求证: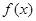 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当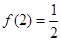 时,解不等式
时,解不等式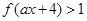 .
.