若 ,则点
,则点 位于( )
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
化简 ( )
( )
A. |
B. |
C. |
D. |
下列说法正确的是( )
A.函数 在区间 在区间 内单调递增 内单调递增 |
B.函数 的最小正周期为 的最小正周期为 |
C.函数 的图象是关于点 的图象是关于点 成中心对称的图形 成中心对称的图形 |
D.函数 的图象是关于直线 的图象是关于直线 成轴对称的图形 成轴对称的图形 |
设 为不重合的平面,
为不重合的平面, 为不重合的直线,则下列命题正确的是( )
为不重合的直线,则下列命题正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
在 中,内角
中,内角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, 若
若 ,
,
 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
等差数列 的通项公式是
的通项公式是 ,其前
,其前 项和为
项和为 ,则数列
,则数列 的前11项和为( )
的前11项和为( )
A. |
B. |
C. |
D. |
已知数列 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前 项和
项和 有最大值,则使
有最大值,则使 的
的 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
设变量 ,
, 满足
满足 ,则
,则 的最大值和最小值分别为( )
的最大值和最小值分别为( )
| A.1,-1 | B.2,-2 | C.1,-2 | D.2,-1 |
若 ,
, ,且
,且 ,则
,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如图所示,则该几何体的俯视图为( )

已知角 的终边落在直线
的终边落在直线 (
( )上,则
)上,则 。
。
在 中,
中, ,
, ,则
,则 的最大值为 。
的最大值为 。
 中,
中, ,
, ,
, ,则符合条件的三角形有 个。
,则符合条件的三角形有 个。
已知 的一个内角为
的一个内角为 ,并且三边长构成公差为
,并且三边长构成公差为 的等差数列,则
的等差数列,则 的面积为 。
的面积为 。
在等差数列 中,
中, ,则
,则 。
。
已知 ,
, ,且
,且 ,
, ,
, 成等比数列,则
成等比数列,则 的最小值 。
的最小值 。
下面关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;
③若四个侧面两两全等,则该四棱柱为直四棱柱;
④若四棱柱的四条体对角线两两相等,则该四棱柱为直四棱柱。
其中,真命题的编号是 (写出所有真命题的编号)。
已知函数 ,且
,且 ,
, 。
。
(1)求 的最小正周期;
的最小正周期;
(2)求 的单调递减区间;
的单调递减区间;
(3)函数 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足

 。
。
(1)求角 的大小;
的大小;
(2)若 ,
, ,试判断
,试判断 的形状,并说明理由
的形状,并说明理由
已知数列 满足:
满足: ,
, (
( )。数列
)。数列 满足
满足
( )。
)。
(1)若 是等差数列,且
是等差数列,且 ,求
,求 的值及
的值及 的通项公式;
的通项公式;
(2)若 是等比数列,求
是等比数列,求 的前
的前 项和
项和
设 ,求
,求 在
在 上的最大值和最小值
上的最大值和最小值
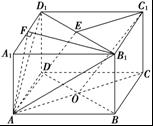
如图在三棱柱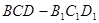 与四棱锥
与四棱锥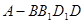 的组合体中,已知
的组合体中,已知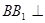 平面
平面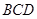 ,四边形
,四边形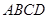 是平行四边形,
是平行四边形,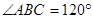 ,
,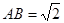 ,
,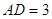 ,
,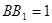 。
。
(1)设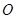 是线段
是线段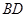 的中点,求证:
的中点,求证: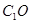 ∥平面
∥平面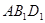 ;
;
(2)求直线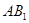 与平面
与平面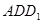 所成的角。
所成的角。