不等式 的解集为 ;
的解集为 ;
在 中,
中, 则
则 等于 ;
等于 ;
在等比数列 中,
中, ,则
,则 = ;
= ;
已知 ,且
,且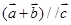 ,则实数
,则实数 的值为 ;
的值为 ;
已知四个正数1,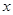 ,
,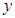 ,3中,前三个数成等比数列,后三个数成等差数列,则
,3中,前三个数成等比数列,后三个数成等差数列,则 = ;
= ;
已知向量 ,则
,则 = ;
= ;
若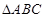 的三个内角
的三个内角 满足
满足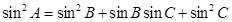 ,则
,则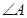 = ;
= ;
若向量 ,则
,则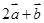 与
与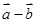 的夹角等于 ;
的夹角等于 ;
在三角形ABC中,有如下命题,其中正确命题的序号是 ;
(1).若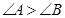 ,则
,则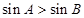 ;(2)若
;(2)若 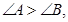 则
则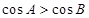 ;
;
(3)若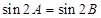 ,则A=B; (4) 若
,则A=B; (4) 若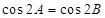 ,则A=B
,则A=B
若 的三个内角
的三个内角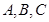 成等差数列,且
成等差数列,且 ,则
,则 的形状为 ;
的形状为 ;
在2011年9月28日成功发射了“天宫一号”,假设运载火箭在点火第一秒钟通过的路程为 ,以后每秒通过的路程都增加
,以后每秒通过的路程都增加 ,达到离地面
,达到离地面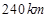 的高度时,火箭与飞船分离,这一过程需要的时间大约是 秒钟;
的高度时,火箭与飞船分离,这一过程需要的时间大约是 秒钟;
在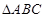 中,角
中,角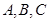 所对的边分别是
所对的边分别是 ,若
,若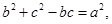 且
且 则角
则角 = ;
= ;
已知等差数列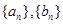 的前n项和分别为
的前n项和分别为 和
和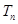 ,若
,若 ,且
,且 ,则n的值为__________.
,则n的值为__________.
已知数列{ }是等差数列,平面内三点A、B、C共线,且
}是等差数列,平面内三点A、B、C共线,且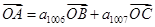 则数列{
则数列{ }的前2012项和
}的前2012项和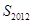 = ;
= ;
已知正项等比数列
(1)求数列 的通项公式;
的通项公式;
(2)若 分别是等差数列
分别是等差数列 的第3项和第5项,求数列
的第3项和第5项,求数列 的通项公式及前n项和
的通项公式及前n项和
已知 ,
,  , 当k为何值时:
, 当k为何值时:
(1)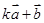 与
与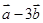 垂直?
垂直?
(2)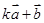 与
与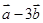 平行? 是同向还是反向?
平行? 是同向还是反向?
(3)试用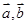 表示
表示 。
。
在 中,角
中,角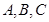 所对的边分别是
所对的边分别是 ,且
,且
(1)求角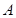 ;
;
(2)若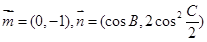 ,试求
,试求 的最小值.
的最小值.
已知数列 的前
的前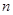 项和
项和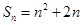 ,设数列
,设数列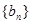 满足
满足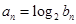 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求数列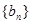 的前
的前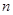 项和
项和 ;
;
(3)设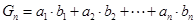 ,求
,求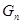 .
.
如图,有两条相交成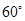 角的直路
角的直路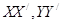 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在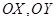 上,起初甲离
上,起初甲离 点
点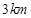 ,乙离
,乙离 点
点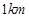 ,后来甲沿
,后来甲沿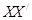 的方向,乙沿
的方向,乙沿 的方向,同时以
的方向,同时以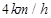 的速度步行。
的速度步行。
(1)起初两人的距离是多少?
(2)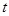 小时后两人的距离是多少?
小时后两人的距离是多少?
(3)什么时候两人的距离最短,并求出最短距离。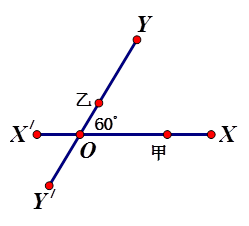
已知二次函数 满足条件:
满足条件:
① ;②
;② 的最小值为
的最小值为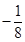 。
。
(1)求函数 的解析式;
的解析式;
(2)设数列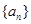 的前
的前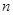 项积为
项积为 ,且
,且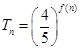 ,求数列
,求数列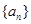 的通项公式;
的通项公式;
(3)在(2)的条件下,若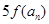 是
是 与
与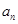 的等差中项,试问数列
的等差中项,试问数列 中第几项的值最小?求出这个最小值。
中第几项的值最小?求出这个最小值。