2012年全国统一高考理科数学试卷（上海卷）

计算： $\frac{3-i}{1+i}$=（ $i$为虚数单位）.

若集合 $A=\left\{\overline{)x}2x+1>0\right\}$， $B=\left\{\overline{)x}\left|x-1\right|<2\right\}$，则 $A\cap B=$.

函数 $f\left(x\right)=\left|\begin{array}{cc}2& \cos x\\ sixn& -1\end{array}\right|$的值域是.

若 $\stackrel{\rightharpoonup }{n}=(-2,1)$是直线 $l$的一个法向量，则 $l$的倾斜角的大小为（结果用反三角函数值表示）.

在 ${\left(x-\frac{2}{x}\right)}^6$的二项展开式中,常数项等于.

有一列正方体，棱长组成以1为首项， $\frac{1}{2}$为公比的等比数列，体积分别记为 $V_1,V_2,...,V_n,...$，则 $\underset{n\to +\infty }{lim}(V_1+V_2+...+V_n)=$.

已知函数 $f\left(x\right)=e^{x-a}$（ $a$为常数）.若 $f\left(x\right)$在区间 $[1,+\infty )$上是增函数，则 $a$的取值范围是.

若一个圆锥的侧面展开图是面积为 $2p$的半圆面，则该圆锥的体积为.

已知 $y=f\left(x\right)+x^2$是奇函数，且 $f\left(1\right)=1$.若 $g\left(x\right)=f\left(x\right)+2$，则 $g(-1)=$.

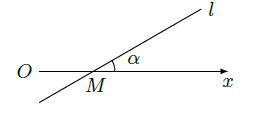
如图，在极坐标系中，过点 $M(2,0)$的直线 $l$与极轴的夹角 $\alpha =\frac{\pi }{6}$.若将 $l$的极坐标方程写成 $\rho =f\left(\theta \right)$的形式，则 $f\left(\theta \right)=$.

三位同学参加跳高、跳远、铅球项目的比赛.若每人都选择其中两个项目，则有且仅有
两人选择的项目完全相同的概率是   （结果用最简分数表示）.

在平行四边形 $ABCD$中， $\angle A=\frac{\pi }{3}$, 边 $AB$、 $AD$的长分别为2、1. 若 $M$、 $N$分别是边 $BC$、 $CD$上的点，且满足 $\frac{\left|\stackrel{\rightharpoonup }{BM}\right|}{\left|\stackrel{\rightharpoonup }{BC}\right|}=\frac{\left|\stackrel{\rightharpoonup }{CN}\right|}{\left|\stackrel{\rightharpoonup }{CD}\right|}$，则 $\stackrel{\rightharpoonup }{AM}·\stackrel{\rightharpoonup }{AN}$的取值范围是.

已知函数 $y=f\left(x\right)$的图像是折线段 $ABC$，若中 $A(0,0),B(\frac{1}{2},5),C(1,0)$.函数 $y=xf\left(x\right)(0\le x\le 1)$的图像与 $x$轴围成的图形的面积为.

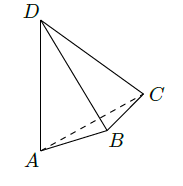
如图， $AD$与 $BC$是四面体 $ABCD$中互相垂直的棱， $BC=2$. 若 $AD=2c$，且 $AB+BD=AC+CD=2a$，其中 $a$、 $c$为常数，则四面体 $ABCD$的体积的最大值是.

若 $1+\sqrt{2}i$是关于 $x$的实系数方程 $x^2+bx+c=0$的一个复数根，则（  ）

在 $△ABC$中，若 ${\sin }^{2}A+{\sin }^{2}B<{\sin }^{2}C$，则 $△ABC$的形状是（   ）

设 $10\le x_1\le x_2\le x_3\le x_4\le {10}^4,x^5={10}^5$,随机变量 $\xi 1$取值 $x_1$、 $x_2$、 $x_3$、 $x_4$、 $x_5$的概率均为0.2，随机变量 ${\xi }_2$取值 $\frac{x_1+x_2}{2}$、 $\frac{x_2+x_3}{2}$、 $\frac{x_3+x_4}{2}$、 $\frac{x_4+x_5}{2}$、 $\frac{x_5+x_6}{2}$的概率也为0.2.若记 $D{\xi }_1$、 $D{\xi }_2$分别为 ${\xi }_1$、 ${\xi }_2$的方差，则（）

设 $a_n=\frac{1}{n}\sin \frac{n\pi }{25}$， $S_n=a_1+a_2+...+a_n$. 在 $S_1,S_2,...S_{100}$中，正数的个数是（  ）

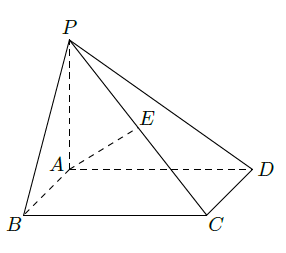
如图，在四棱锥 $P-ABCD$中，底面 $ABCD$是矩形， $PA\perp \mathrm{底面}ABCD$， $E$是 $PC$的中点.已知 $AB=2$， $AD=2\sqrt{2}$， $PA=2$.求：

（1）三角形 $PCD$的面积；
（2）异面直线 $BC$与 $AE$所成的角的大小.

已知函数 $f\left(x\right)=lg\left(x+1\right)$.
（1）若 $0<f\left(1-2x\right)-f\left(x\right)<1$，求 $x$的取值范围；
（2）若 $g\left(x\right)$是以2为周期的偶函数，且当 $0\le x\le 1$时，有 $g\left(x\right)=f\left(x\right)$，求函数 $y=g\left(x\right)$ $\left(x\in \left[1,2\right]\right)$的反函数.

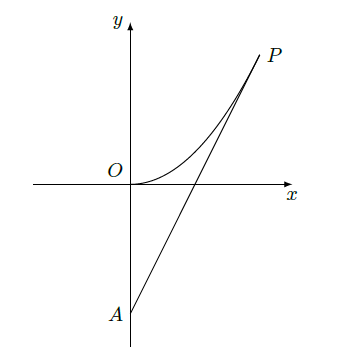
海事救援船对一艘失事船进行定位：以失事船的当前位置为原点，以正北方向为 $y$轴正方向建立平面直角坐标系（以1海里为单位长度），则救援船恰在失事船的正南方向12海里 $A$处，如图. 现假设：①失事船的移动路径可视为抛物线 $y=\frac{12}{49}{x}^2$；②定位后救援船即刻沿直线匀速前往救援；③救援船出发 $t$小时后，失事船所在位置的横坐标为.

（1）当 $t=0.5$时，写出失事船所在位置 $P$的纵坐标. 若此时两船恰好会合，求救援船速度的大小和方向；
（2）问救援船的时速至少是多少海里才能追上失事船？

在平面直角坐标系 $xOy$中，已知双曲线 $C_1:2x^2-y^2=1$.
（1）过 $C_1$的左顶点引 $C_1$的一条渐近线的平行线，求该直线与另一条渐近线及 $x$轴围成的三角形的面积；
（2）设斜率为1的直线 $l$交 $C_1$于 $P$. $Q$两点，若 $l$与圆 $x^2+y^2=1$相切，求证： $OP\perp OQ$；
（3）设椭圆 $C_2:4x^2+y^2=1$. 若 $M,N$分别是 $C_1$、 $C_2$上的动点，且 $OM\perp ON$，求证： $O$到直线 $MN$的距离是定值.

对于数集 $X=\left\{-1,x_1,x_{2,}\dots ,x_n\right\}$，其中 $0<x_x<x_2<\dots <x_n$， $n\ge 2$，定义向量集 $Y=\left\{\overline{)\underset{a}{\to }}\underset{a}{\to }=\left(s,t,s\in X,t\in X\right)\right\}$. 若对于任意 $\underset{a_1}{\to }\in Y$，存在 $\underset{a_2}{\to }\in Y$，使得 $\underset{a_1}{\to }.\underset{a_2}{\to }=0$，则称X具有性质 $P$.例如 $X=\left\{-1,1,2\right\}$具有性质 $P$.
（1）若 $x>2$，且 $\left\{-1,1,2,x\right\}$，求 $x$的值；
（2）若 $X$具有性质 $P$，求证： $1\in X$,且当 $x_n>1$时， $x_1=1$；
（3）若 $X$具有性质 $P$，且 $x_1=1,x_2=q$（ $q$为常数），求有穷数列 $x_1,x_2,\dots ,x_n$的通项公式.