集合 , ,则 ()
| A. | B. | C. | D. |
下列函数中,既是奇函数又是增函数的为( )
| A. | B. | C. | D. |
对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是()
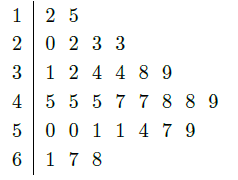
| A. | 46,45,56 | B. | 46,45,53 |
| C. | 47,45,56 | D. | 45,47,53 |
设 , 是虚数单位,则 是"复数 为纯虚数"的()
| A. | 充分不必要条件 | B. | 必要不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
下图是计算某年级500名学生期末考试(满分为100分)及格率
的程序框图,则图中空白框内应填入( )
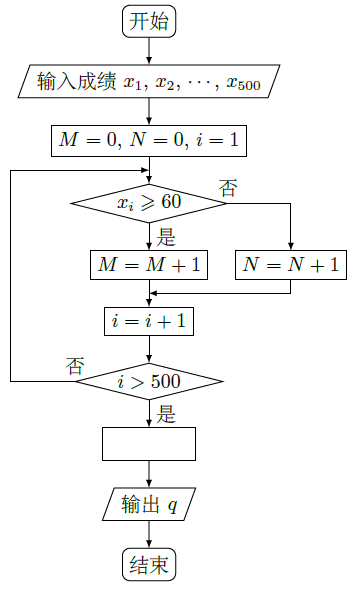
| A. | B. | ||
| C. | D. |
已知圆 , 过点 的直线,则()
| A. | 与 相交 | B. | 与 相切 |
| C. | 与 相离 | D. | 以上三个选项均有可能 |
设向量 与 垂直,则 等于()
| A. | B. | C. | 0 | D. | -1 |
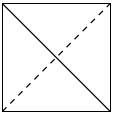
将正方形(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )
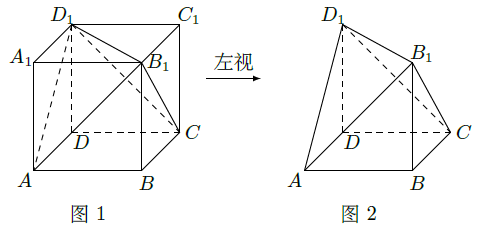
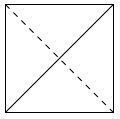


设函数 则()
| A. | 为 的极大值点 | B. |
为
的极小值点 |
| C. | 为 的极大值点 | D. | 为 的极小值点 |
小王从甲地到乙地的时速分别为 ,其全程的平均时速为 ,则()
| A. | B. | C. | D. |
设函数发 ,则 .
观察下列不等式
,
……
照此规律,第五个不等式为
在三角形 中,角 所对应的长分别为 ,若 , , ,则 .
如图是抛物线形拱桥,当水面在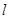 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
若存在实数 使 成立,则实数 的取值范围是.
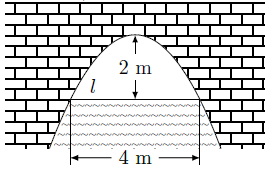
如图,在圆 中,直径 与弦 垂直,垂足为 , ,垂足为 ,若 , ,则 .
直线 与圆 相交的弦长为.
已知等比数列
的公比为
.
(1)若
=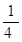 ,求数列
的前
项和;
,求数列
的前
项和;
(Ⅱ)证明:对任意
,
,
,
成等差数列.
函数
的最大值为3, 其图像相邻两条对称轴之间的距离为
,
(1)求函数
的解析式;
(2)设
,则
,求
的值
直三棱柱
中,
.

(Ⅰ)证明
;
(Ⅱ)已知
,求三棱锥
的体积.
假设甲乙两种品牌的同类产品在某地区市场上销售量相等,为了解他们的使用寿命,现从两种品牌的产品中分别随机抽取100个进行测试,结果统计如下: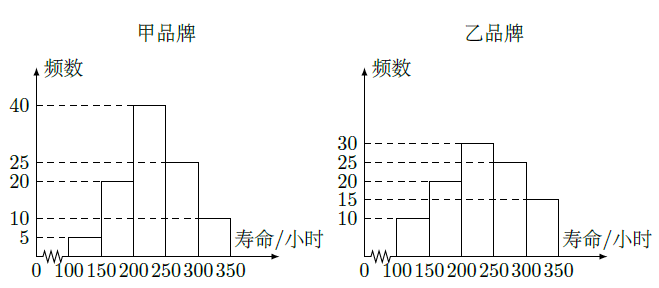
(Ⅰ)估计甲品牌产品寿命小于200小时的概率;
(Ⅱ)这两种品牌产品中,某个产品已使用了200小时,试估计该产品是甲品牌的概率.
已知椭圆
,
以
的长轴为短轴,且与
有相同的离心率。
(1)求椭圆
的方程;
(2)设
为坐标原点,点
分别在椭圆
和
上,
,求直线
的方程.
设函数
(1)设
,
,
,证明:
在区间
内存在唯一的零点;
(2)设
为偶数,
,
,求
的最小值和最大值;
(3)设
,若对任意
,有
,求
的取值范围;