已知数列的一个通项公式为
，则
（ ）
A． |
B． |
C． |
D． |
在
中，若
，则
与
的大小关系为（ ）
A． |
B． |
C． |
D．、的大小关系不能确定 |
设等比数列
的前
项和为
，若
，则
（ ）
A． |
B． |
C． |
D． |
若数列
的通项公式为
，则（ ）
| A．为递增数列 | B．为递减数列 |
| C．从某项后为递减数列 | D．从某项后为递增数列 |
已知
，且
，则
的最小值为（ ）
A． |
B． |
C． |
D． |
在
中，若
，则的形状是（ ）
| A．等腰三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等腰或直角三角形 |
已知
为等差数列且
，则（ ）
A． |
B． |
C． |
D． |
若
且
，则下列不等式恒成立的为（ ）
A． |
B． |
C． |
D． |
已知数列
、
都是公差为1的等差数列，其首项分别为
，且
设
，则数列
的前10项和等于（ ）
| A．55 | B．70 | C．85 | D．100 |
已知
内接于单位圆，且面积为
，则长为
的三条线段（ ）
| A．不能构成三角形 |
B．能构成一个三角形，其面积为 |
| C．能构成一个三角形，其面积大于 |
| D．能构成一个三角形，其面积小于 |
等比数列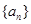
中，
，则
的值为 ．
在
中，
，则此三角形的最大边的长为 ．
已知数列
是首项为1，公比为
的等比数列，则
．
已知
，则
取值范围是 ．
为等差数列，若
，则使前
项
的最大自然数是 ．
在数列
中，
，当
时，
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，求数列
的前
项和
.
在
中，
是三角形的三内角，
是三内角对应的三边，已知成等差数列，成等比数列
（Ⅰ）求角
的大小；
（Ⅱ）若
，求
的值.
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示）.如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米2，水池所有墙的厚度忽略不计，试设计污水处理池的长和宽，使总造价最低，并求出最低总造价。
已知等比数列
中，
，且
，公比
，（1）求
；（2）设
，求数列
的前
项和
在
中，已知
，面积
，
（1）求的三边的长；
（2）设
是（含边界）内的一点，到三边
的距离分别是
①写出所满足的等量关系；
②利用线性规划相关知识求出
的取值范围.
数列
首项
，前
项和
满足等式
（常数
，
……）
（1）求证：为等比数列；
（2）设数列的公比为
，作数列
使
（……），求数列的通项公式.
（3）设
，求数列
的前项和
.