当 ______时,二次根式
______时,二次根式 在实数范围内有意义.
在实数范围内有意义.
计算 _______.
_______.
方程 的根为_______.
的根为_______.
如果最简二次根式 与
与 能合并,则
能合并,则 _______.
_______.
坐标平面内点P( ,2)与点Q(3,-2)关于原点对称,则
,2)与点Q(3,-2)关于原点对称,则 _______.
_______.
图(1)中的梯形符合_______条件时,可以经过旋转和翻折形成图案(2).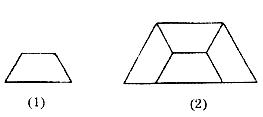
若方程 是关于
是关于 的一元二次方程,则
的一元二次方程,则 的取值范围是_______.
的取值范围是_______.
如图,BD是⊙O的直径,∠A=30°,则∠CBD=_________.
在平面直角坐标系中,半径为5的⊙O与 轴交于A(-2,0),B(4,0),则圆心点M的坐标为
轴交于A(-2,0),B(4,0),则圆心点M的坐标为
受全球金融危机影响,在最近一个月内猪肉价格两次下降,由原来每斤l6元下调到每斤9元,求平均每次下调的百分率为_____________.
下列各图是一些交通标志的图案,其中是中心对称图形的是
若 ,
, 为实数,且
为实数,且 ,则
,则 的值为
的值为
| A.1 | B.2011 | C.-l | D.-2011 |
如图,△ABC的三个顶点都在5 × 5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形的面积是_______平方单位(结果保留 ).
).
A. |
B. |
C. |
D. |
关于 的方程
的方程 。有实数根,则
。有实数根,则 满足
满足
A. ≥1 ≥1 |
B. >1且 >1且 ≠5 ≠5 |
C. ≥1且 ≥1且 ≠5 ≠5 |
D. ≠5 ≠5 |
如图,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有
| A.内切、相交 | B.外离、相交 | C.外切、外离 | D.外离、内切 |
如图,在4×4的正方形网格中,△MNP绕某点旋转90°,得到△M1N1P1,则其旋转中心可以是
| A.点E | B.点F | C.点G | D.点H |
解方程:
计算: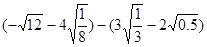
先化简,再求值. ,其中
,其中 ,
,
对于竖直向上抛的物体,在没有空气阻力的条件下,满足这样的关系式: ,其中
,其中 是上升高度,
是上升高度, 是初速度,
是初速度, 是重力加速度(本题中取
是重力加速度(本题中取 ),
), 是抛出后所经过的时间,一物体以
是抛出后所经过的时间,一物体以 的初速度竖直向上抛出,物体何时在离抛出点25m高的地方?
的初速度竖直向上抛出,物体何时在离抛出点25m高的地方?
如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,求⊙O的半径。
下图是4×4的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=2.
(1)用尺规作图,作出△ABC绕点A逆时针旋转60°后得到的AB1Cl(不写画法,保留图画痕迹);
结论:__________为所求.
(2)在(1)的条件下,连接B1C,求B1C的长.
列方程解应用题:
如图,有一块矩形纸板,长为20 ,宽为14
,宽为14 ,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起;就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为160
,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起;就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为160 ,那么纸板各角应切去边长为多大的正方形?
,那么纸板各角应切去边长为多大的正方形?
AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
两个大小相同且含30°角的三角板ABC和DEC如图(1)摆放,使直角顶点重合.将图(1)中△DEC绕点C逆时针旋转30°得到图(2),点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
(1)不添加辅助线,写出图(2)中所有与△BCF全等的三角形;
(2)将图(2)中的△DEC绕点C逆时针旋转45°得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图(3),探究线段D1F1与AH1之间的数量关系,并写出推理过程;
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I=CI.
如图:点A、B在直线MN上,AB=11厘米,⊙A、⊙B的半径均为1厘米,⊙A以每秒2厘米的速度自左向右运动,于此同时,⊙B的半径也不断增大,其半径 (厘米)与时间
(厘米)与时间 (秒)之间的关系式为
(秒)之间的关系式为 (
( ≥0).
≥0).
(1)试写出点A、B之间的距离 (厘米)与时间
(厘米)与时间 (秒)之间的函数表达式.
(秒)之间的函数表达式.
(2)问点A出发后多少秒两圆相切?
已知关于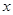 的一元二次方程
的一元二次方程 .
.
(1)求证:当 取不等于l的实数时,此方程总有两个实数根.
取不等于l的实数时,此方程总有两个实数根.
(2)若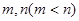 是此方程的两根,并且
是此方程的两根,并且 ,直线
,直线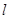 :
: 交
交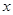 轴于点A,交
轴于点A,交 轴于点B,坐标原点O关于直线
轴于点B,坐标原点O关于直线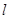 的对称点O′在反比例函数
的对称点O′在反比例函数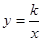 的图象上,求反比例函数
的图象上,求反比例函数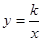 的解析式.
的解析式.
(3)在(2)的成立的条件下,将直线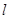 绕点A逆时针旋转角
绕点A逆时针旋转角 ,得到直线
,得到直线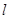 ′,
′,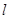 ′交
′交 轴于点P,过点P作
轴于点P,过点P作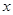 轴的平行线,与上述反比例函数
轴的平行线,与上述反比例函数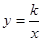 的图象交于点Q,当四边形APQO′的面积为
的图象交于点Q,当四边形APQO′的面积为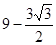 时,求角
时,求角 的值.
的值.