若 且
且 ,则下列不等式中一定成立的是
,则下列不等式中一定成立的是
A. |
B. |
C. |
D. |
设数列 ,
, ,
, ,
, ,…,则
,…,则 是这个数列的
是这个数列的
| A.第6项 | B.第7项 | C.第8项 | D.第9项 |
已知条件 ,条件
,条件 ,则
,则 是
是 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
(理)在等差数列{an}中,已知a5=3,a9=6,则a13=
| A.9 | B.12 | C.15 | D.18 |
(文)1与5两数的等差中项是
| A.1 | B.3 | C.2 | D. |
椭圆 上一点P到一个焦点的距离为5,则P到另一个焦点的距离为
上一点P到一个焦点的距离为5,则P到另一个焦点的距离为
| A.10 | B.6 | C.5 | D.4 |
已知 中,
中, 所对的边分别为
所对的边分别为 ,且
,且 ,那么角
,那么角 等于
等于
A. |
B. |
C. |
D. |
若实数 满足
满足 则
则 的最小值是
的最小值是
| A.0 | B. |
C.1 | D.2 |
抛物线  的准线方程是
的准线方程是
A. |
B. |
C. |
D. |
(理)如图,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成角的余弦值为
A. |
B. |
C. |
D. |
(文)曲线 在点
在点 处的切线方程是
处的切线方程是
A. |
B. |
C. |
D. |
已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点, ,P为C的准线上一点,则
,P为C的准线上一点,则 的面积为
的面积为
| A.18 | B.24 | C.36 | D.48 |
命题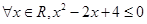 的否定为
的否定为
已知双曲线的方程为 ,则它的离心率为______.
,则它的离心率为______.
.函数 的定义域是
的定义域是
等比数列 中
中 ,且
,且 ,则
,则 = .
= .
曲线 是平面内与两个定点
是平面内与两个定点 和
和 的距离的积等于常数
的距离的积等于常数 的点的轨迹,给出下列三个结论:
的点的轨迹,给出下列三个结论:
①曲线 过坐标原点;
过坐标原点;
②曲线 关于坐标原点对称;
关于坐标原点对称;
③若点 在曲线
在曲线 上,则
上,则 的面积不大于
的面积不大于 .
.
其中,所有正确结论的序号是____ _____
(本小题满分7分)
在△ 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .
.
(1)求 的值; (2)求
的值; (2)求 的值.
的值.
(本小题满分7分)
已知等差数列{ }的前n项和为Sn,且
}的前n项和为Sn,且 bn=
bn=
 -30
-30
(1)求通项 ; (2)求数列{bn}的前n项和Tn的最小值。
; (2)求数列{bn}的前n项和Tn的最小值。
某车间生产某机器的两种配件A和B,生产配件A成本费y 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?

(理)如图,P—ABCD是正四棱锥, 是正方体,其中
是正方体,其中

(1)求证: ;
;
(2)求平面PAD与平面 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(文)已知 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求函数的单调区间;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分10分)
.设数列 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设 ,求证:数列
,求证:数列 是等比数列,并求出
是等比数列,并求出 的通项公式。
的通项公式。
(2)求数列 的前n项和.
的前n项和.