已知复数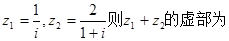
A.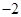 |
B.2 | C. |
D. |
“ ”是“
”是“ ”成立的
”成立的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知函数 的反函数为
的反函数为 ,则
,则 =
=
| A.1 | B.2 | C.3 | D.4 |
在等差数列 中,
中, ,其前n项
,其前n项 ,则n=
,则n=
| A.7 | B.8 | C.15 | D.17 |
已知向量 ,
, ,若
,若 ,则
,则
A. |
B. |
C.1 | D.3 |
若把函数 的图象向右平移
的图象向右平移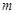 (
(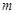 >0)个单位长度,使点
>0)个单位长度,使点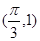 为其对称中心,则
为其对称中心,则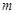 的最小值是
的最小值是
A.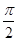 |
B. |
C. |
D. |
已知A、B、C三点在球心为 ,半径为3的球面上,且三棱锥
,半径为3的球面上,且三棱锥 —ABC为正四面体,那么A、B两点间的球面距离为
—ABC为正四面体,那么A、B两点间的球面距离为
A、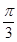 B、
B、 C、
C、 D、
D、
已知圆 上两点
上两点 关于直线
关于直线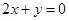 对称,则圆
对称,则圆 的半径为
的半径为
| A.9 | B.3 | C.6 | D.2 |
已知 ,
, 是不同的平面,
是不同的平面, ,
, 是不同的直线,给出下列命题:
是不同的直线,给出下列命题:
①若 ,则
,则 ;
;
②若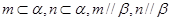 ,则
,则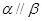 ;
;
③若 是异面直线,则
是异面直线,则 与
与 相交;
相交;
④若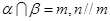 ,且
,且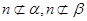 ,则
,则 .
.
其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知函数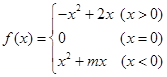 为奇函数,若函数
为奇函数,若函数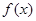 在区间
在区间 上单调递增,则
上单调递增,则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
双曲线 的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率为
相切,则该双曲线的离心率为
A. |
B.2 | C.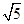 |
D. |
函数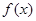 在定义域
在定义域 内可导,若
内可导,若 ,且当
,且当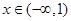 时,
时,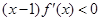 ,设
,设 ,
,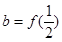 ,
,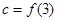 ,则
,则
A.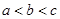 |
B.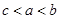 |
C. |
D.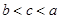 |
若二项式 的展开式中各项系数的和是64,则展开式中的常数项为 .
的展开式中各项系数的和是64,则展开式中的常数项为 .
已知随机变量 服从正态分布
服从正态分布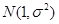 ,
, ,
, ,则实数
,则实数 ___________.
___________.
连掷两次骰子得到的点数分别为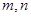 .记向量
.记向量 与向量
与向量 的夹角为
的夹角为 ,则
,则 的概率是_______________.
的概率是_______________.
已知变量 满足
满足 ,则
,则 的最大值为_____.
的最大值为_____.
(本小题满分10分)
在△ABC中,角A、B、C对边分别是 ,且满足
,且满足 .
.
(1)求角A的大小;
(2)求 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
(本小题满分12分)
在一次人才招聘会上,有 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
(1)求该技术人员被录用的概率;
(2)设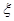 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求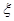 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
在直三棱柱中, 是
是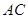 中点.
中点.
(1)求证: //平面
//平面 ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
已知数列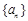 的前n项和为
的前n项和为 ,且
,且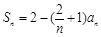 (
(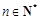 ),
),
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列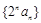 的前n项和为
的前n项和为 ,
,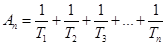 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分12分)
已知椭圆
 的离心率为
的离心率为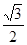 ,直线
,直线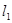 经过椭圆的上顶点
经过椭圆的上顶点 和右顶点
和右顶点 ,并且和圆
,并且和圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设直线
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,以线段
两点,以线段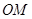 ,
, 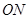 为邻边作平行四边行
为邻边作平行四边行 ,其中顶点
,其中顶点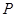 在椭圆
在椭圆 上,
上, 为坐标原点,求
为坐标原点,求 的取值范围.
的取值范围.
(本小题满分12分)
已知函数
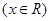 (
( 是自然对数的底数,
是自然对数的底数,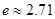 ).
).
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)证明 对一切
对一切 恒成立.
恒成立.