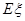的逆矩阵为 .
一枚硬币连续抛掷两次，出现一次正面一次反面的概率为 .
在二项式
的展开式中，含
的项的系数是 .
已知某一随机变量X的概率分布表如右图，且E(X)＝3，则V(X)＝ 
| X |
0 |
a |
6 |
| P |
0.3 |
0.6 |
b |
从1、2、3、4、5、6六个数中选出两位奇数和两位偶数组成无重复数字的四位数，要求两位偶数相邻，则共有 个这样的四位数（以数字作答）.
从5名男生和3名女生中选出3人参加学校组织的演讲比赛，则选出的3人中既有男生又有女生的不同选法共有 种（以数字作答）.
从装有3个红球，3个白球的袋中随机取出2个球，设其中有
个红球，则
=
若某同学把英语单词“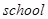
”的字母顺序写错了，则可能出现的错误写法共有
种（以数字作答）.
设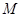
是把坐标平面上的点的横坐标伸长为原来的4倍，纵坐标伸长为原来的3倍的伸压变换，则圆
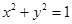在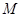的作用下的新曲线的方程是
从红桃2、3、4、5和梅花2、3、4、5这8张扑克牌中取出4张排成一排，如果取出的4张扑克牌所标的数字之和等于14，则不同的排法共有 种（以数字作答）.
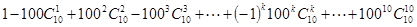除以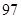
的余数是_______.
从编号为1、2、3、4的四个不同小球中取出三个不同的小球放入编号为1、2、3的三个不同盒子里，每个盒子放一个球，则1号球不放1号盒子，3号球不放3号盒子的放法共有 种（以数字作答）.
如图，矩形
的
在变换
的作用下分别变成
，形成了平行四边形
（1）求变换对应的矩阵
；
（2）变换对应的矩阵将直线
变成了直线
：
，求直线的（1）方程.
某次春游活动中，
名老师和6名同学站成前后两排合影，名老师站在前排，6名同学站在后排．
（１）若甲，乙两名同学要站在后排的两端，共有多少种不同的排法？
（２）若甲，乙两名同学不能相邻，共有多少种不同的排法？
（３）若甲乙两名同学之间恰有两名同学，共有多少种不同的排法？
（4）在所有老师和学生都排好后，拍照的师傅觉得队形不合适，遂决定从后排6人中抽2人调整到前排．若其他人的相对顺序不变，共有多少种不同的调整方法？
在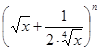
的展开式中，前三项系数成等差数列，求
（1）展开式中所有项的系数之和；
（2）展开式中的有理项 ；
（3）展开式中系数最大的项
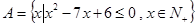已知集合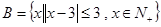
，集合
，集合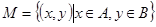
（1）求从集合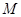
中任取一个元素是
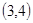的概率；
（2）从集合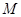中任取一个元素，求
的概率；
（3）设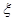
为随机变量，
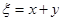，写出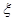的概率分布，并求