若
下列不等式成立的是 ( )
不等式（x+2）(1－x)>0的解集是（ ）
| A．｛ｘ｜ｘ＜－２或x>1｝ | B．｛ｘ｜x<－１或ｘ>２｝ |
| C．｛ｘ｜－2＜ｘ＜1｝ | D．｛ｘ｜－１＜ｘ＜２｝ |
已知三条直线
，
，
，三个平面
，
，
．下面四个命题中，正确的是（）
A． |
B． |
C． |
D． |
如右图,一几何体的三视图：则这个几何体是（ ）
Com
| A．圆柱 | B．空心圆柱 |
| C．圆 锥 | D．圆台 |
不等式
表示的平面区域在直线
的（ ）
| A．右上方 | B．右下方 | C．左上方 | D．左下方 |
如右图所示，
是圆
的直径，
是异于
，
两点的圆周上的任意一点，
垂直于圆所在的平面，则
，
，
，
中，直角三角形的个数是（ ）
A． |
B． |
C． |
D． |
四面体
中，各个面都是边长为
的正三角形，
分别是
和
的中 点，则异面直线
与
所成的角等于（ ）
A 
B 
C 
D 
长方体的一个顶点上三条棱的边长分别为3、4、5，且它的八个顶点都在同一个球面上，这个球的表面积是（ ）
A．  |
B． |
C． |
D． |
在下列四个正方体中，能得出异面直线AB⊥CD的是( ) 
已知a、b∈（0，1）且a≠b，下列各式中最大的是（ ）
| A．a2+b2 | B．２ |
C．2 b |
D．+b[来 |
下面四个命题：
① 若直线
平面
，则内任何直线都与
平行；
② 若直线
平面，则内任何直线都与垂直；
③ 若平面
平面
，则内任何直线都与平行；
④ 若平面
平面，则内任何直线都与垂直．
其中正确的两个命题是（ ）
| A．①与② | B．②与③ | C．③与④ | D．②与④ |
如图，将无盖正方体纸盒展开，直线AB、CD在原正方体中的位置关系是( ) 
A．平行 B．相交且垂直 C．异面直线 D．相交成60°角
半径为2的半圆卷成一个圆锥，则它的体积为________________.
已知x>1，则函数y＝x+
的最小值是_________．
设一元二次不等式ax2+bx+1>0的解集为｛ｘ｜－1≤ｘ≤
｝，则ab的值是 _____.
如果函数f(x)=x2+(m－1)x+1在区间
上为减函数，则m的取值范围_____.
已知
，
满足约束条件
求
的最小值与最大值。
一个长、宽、高分别为a、b、c长方体的体积是8cm2，它的全面积是32 cm2， 且满足 b2＝ac，求这个长方体所有棱长之和。
如图，直二面角A—BD—C，平面ABD⊥平面BCD,若其中给定 AB="AD" =2，
，
，BC⊥CD .
（Ⅰ）求AC与平面BCD所成的角；
（Ⅱ）求点Ａ到BC的距离．
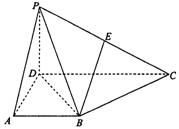
在四棱锥P－ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底 面ABCD是直角梯形，AB∥CD，∠ADC＝90°，AB＝AD＝PD＝1，CD＝2．
(Ⅰ)求证：BE∥平面PAD；
(Ⅱ)求证：BC⊥平面PBD；
(Ⅲ)求四棱锥P－ABCD的体积。
解关于x的不等式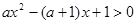
已知26辆货车以相同速度v由A地驶向400千米处的B地，每两辆货车间距离为d千米，现已知d与v的平方成正比，且当v=20（千米／时）时，d=1（千米）．
（1）写出d与v的函数关系；
（2）若不计货车的长度，则26辆货车都到达B地最少需要多少小时？此时货车速度是多少？