复数 的共轭复数是 .
的共轭复数是 .
已知 角的顶点与原点重合,始边与
角的顶点与原点重合,始边与 轴的正半轴重合,终边在直线
轴的正半轴重合,终边在直线 上,则
上,则 .
.
已知命题 ,
, ,则
,则 为 .
为 .
某校共有学生2000名,各年级男、女学生人数如右表示,已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取100人,则应在高三年级中抽取的学生人数为 .
| 年级 |
高一 |
高二 |
高三 |
| 女生 |
385 |
 |
 |
| 男生 |
375 |
360 |
 |
将一颗骰子先后抛掷2次,观察向上的点数,则点数之和是4的倍数的概率是 ,
若 是等差数列{
是等差数列{ }的前n项和,且
}的前n项和,且 ,则
,则 的值为
的值为
函数 (
( 为自然对数的底数)在区间
为自然对数的底数)在区间 上的最大值是 .
上的最大值是 .
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,
是两个不同的平面,
有下列四个命题:
①若 ;
;
② ,则
,则 ;
;
③若 则
则 且
且 ;
;
④若
其中正确的命题是 .(写出所有真命题的序号).
已知双曲线 的渐近线过点
的渐近线过点 ,则该双曲线的离心率为 .
,则该双曲线的离心率为 .
对于函数 若存在
若存在 ,使
,使 成立,则称点
成立,则称点 为函数的不动点,对于任意实数
为函数的不动点,对于任意实数 ,函数
,函数 总有相异不动点,实数
总有相异不动点,实数 的取值范围是____
的取值范围是____
平面直角坐标系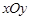 中,已知向量
中,已知向量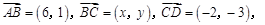 且
且 .
.
(1)求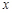 与
与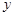 之间的关系式;
之间的关系式;
(2)若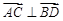 ,求四边形
,求四边形 的面积.
的面积.
如图,在直三棱柱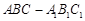 中,
中,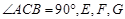 分别是
分别是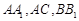 的中点,且
的中点,且 .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面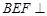 平面
平面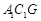 .
.
已知数列 满足:
满足:
(1)求证:数列 是等比数列;
是等比数列;
(2)令 (
( ),如果对任意
),如果对任意 ,都有
,都有 ,
,
求实数 的取值范围.
的取值范围.
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
)
(1)设 ,求证:当
,求证:当 时,
时, ;
;
(2)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实
的最小值是3 ?如果存在,求出实
数a的值;如果不存在,请说明理
已知二阶矩阵M属于特征值3的一个特征向量为 ,并且矩阵
,并且矩阵 对应的变换将点
对应的变换将点 变成点
变成点 ,求出矩阵
,求出矩阵 。
。
已知圆 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 为参数)若直线
为参数)若直线 与圆
与圆 相切,求实数m的值.
相切,求实数m的值.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球;乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,
①摸出3个白球的概率;
②获奖的概率;
(2)求在两次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望 .
.