设
，则
（ ）
A． |
B． |
C． |
D． |
（其中i为虚数单位）在复平面上对应的点位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
设
是虚数单位，则复数
的虚部是 （ ）
A． |
B． |
C． |
D． |
曲线
在点（1，3）处的切线的斜率为 （ ）
A． |
B．1 | C． |
D． |
《论语》云：“名不正，则言不顺；言不顺，则事不成；事不成，则礼乐不兴；礼乐不兴，则刑罚不中；刑罚不中，则民无所措手足；所以名不正，则民无所措手足．”上述推理用的是（ ）
| A．合情推理 | B．归纳推理 | C．类比推理 | D．演绎推理 |
在曲线
上切线倾斜角为
的点是（ ）
| A．(0,0) | B．(2,4) | C． |
D． |
函数
的零点的个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
设函数
，则 （ ）
A． |
B． |
C． |
D． |
函数
的递增区间是（ ）
A．  |
B． |
C． |
D． |
已知
是方程
的一个根，则实数
的值为（ ）
| A．2 | B． |
C．4 | D． |
，则长度等于
的三条线段能构成锐角三角形的充要条件是（ ）
A． |
B． |
C． |
D． |
观察：52 – 1 = 24，72 – 1 = 48，112 – 1 = 120，132 – 1 = 168，… 所得的结果都是24的倍数，继续试验，则有（ ）
| A．第1个出现的等式是：152 – 1 =" 224" |
| B．一般式是：(2n + 3)2 – 1 =" 4(n" + 1)(n+2) |
| C．当试验一直继续下去时，一定会出现等式1012 – 1 =10200 |
| D．24的倍数加1必是某一质数的完全平方 |
已知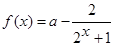
是定义在R上奇函数，则
.
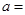；若
.
以函数
为导数的函数
图象过点（9，1），则函数＝____________．
曲线
和
在它们交点处的两条切线与
轴所围成的三角形面积是 .
若对于任意的
, 
恒成立, 则实数a的取值范围是 .
一个九宫格如右表，每个小方格内都填一个复数，它的每行、每列及对角线上三个格内的复数和都相等，则
表示的复数是 .
已知函数
（Ⅰ）求
的单调区间；
（Ⅱ）求
上的最值．
已知复数
，
，
（Ⅰ）求
；
（Ⅱ）若复数
满足
，求
.
设复数
，试求实数
取何值时
（1）Z是实数； （2）Z是纯虚数； （3）Z对应的点位于复平面的第一象限.
已知函数
．
（1）若
在
处取得极值为
，求
的值；
（2）若在
上是增函数，求实数 
的取值范围．
设
，先分别求
，
，
，然后归纳猜想一般性结论，并给出证明.
设函数
，且
为
的极值点．
(Ⅰ) 若为的极大值点，求的单调区间（用
表示）；
(Ⅱ)若
恰有两解，求实数的取值范围．