已知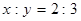 ,下列等式中正确的是( ).
,下列等式中正确的是( ).
A. ; ; |
B.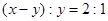 ; ; |
C.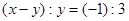 ; ; |
D.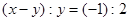 . . |
如图,用放大镜看△ABC,若边BC的长度变为原来的2倍,那么下列说法中,不正确的是( ).
| A.边AB的长度也变为原来的2倍; | B.∠BAC的度数也变为原来的2倍; |
| C.△ABC的周长变为原来的2倍; | D.△ABC的面积变为原来的4倍; |
已知 中,
中, ,若
,若 ,
, ,下列各式中正确的是( ).
,下列各式中正确的是( ).
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
在△ABC中,D、E分别是AB 、AC上的点,下列比例式中不能判定DE∥BC的是( )

若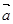 与
与 的方向相反,且,
的方向相反,且,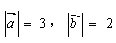 ,则下列用
,则下列用 表示
表示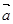 的式子中,正确的是( ).
的式子中,正确的是( ).
如图,在直角坐标平面内,点 与原点
与原点 的距离
的距离 ,线段
,线段 与
与 轴正半轴的夹角为
轴正半轴的夹角为 ,且
,且 ,则点
,则点 的坐标是( ).
的坐标是( ). 
| A.(2,3); | B.(2, ); ); |
C.( ,2); ,2); |
D.(2, ). ). |
已知 是2和6的比例中项,则
是2和6的比例中项,则 .
.
计算:
 .
.
已知: ,且
,且 ,则
,则 的值为 .
的值为 .
已知线段 2cm,点
2cm,点 是线段
是线段 的黄金分割点,且
的黄金分割点,且 >
> ,则线段
,则线段 cm.
cm.
已知 ∽
∽ ,顶点
,顶点 、
、 、
、 分别与
分别与 、
、 、
、 对应,若
对应,若 = 40°,
= 40°, = 60°,
= 60°,
则 =________度.
=________度.
如图,当太阳光与地面成 角时,直立于地面的玲玲测得自己的影长为1.25m,则玲玲的身高约为 m.(精确到0. 01m)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428).
角时,直立于地面的玲玲测得自己的影长为1.25m,则玲玲的身高约为 m.(精确到0. 01m)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428).
如图, 的两条中线
的两条中线 、
、 相交于点G,如果
相交于点G,如果 =2,那么
=2,那么 = .
= .
如图,梯形 中,点
中,点 、
、 分别在边
分别在边 、
、 上,
上,  ∥
∥ ∥
∥ ,
,  ,
,
若 ,
, ,则
,则 = .
= .
右图中的等腰梯形(ABCD)是公园中儿童游乐场的示意图.为满足市民的需求,计划扩建该游乐场. 要求新游乐场以MN为对称轴,且新游乐场与原游乐场相似,相似比为2∶1.又新游乐场的一条边在直线BC上,请你在图中画出新游乐场的示意图.
如图, 在 中, 点D、E分别在BC、AC上,BE平分
中, 点D、E分别在BC、AC上,BE平分 ABC,DE∥BA,若AB="7" ,BC=8.则线段
ABC,DE∥BA,若AB="7" ,BC=8.则线段 的长度为 .
的长度为 .
△ABC中,已知点D在边BC上,且BD=2DC,设 =
= ,
,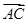 =
=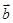 ,则
,则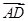 等于 .
等于 .
如图, 中,
中, ,
, ,
, ,
, 是
是 边的中点,
边的中点, 是BC边上一点(点
是BC边上一点(点 不与
不与 、
、 重合),若以
重合),若以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似,则线段
相似,则线段 .
.
如图,点 在平行四边形
在平行四边形 的边
的边 的延长线上,连结
的延长线上,连结 交
交 于点
于点 .求证:
.求证: .
.
如图,已知: . 求证:(1)
. 求证:(1) ;(2)
;(2)  .
.
如图,等边 中,
中, 、
、 、
、 分别是
分别是 、AC、BC上的点,联结
、AC、BC上的点,联结 、EF交于点G,且
、EF交于点G,且 .
.
(1)请直接写出图中所有与 相似的三角形(不用证明);
相似的三角形(不用证明);
(2)若 ,试求
,试求 的值.
的值.
如图,在 中,
中, ,
, ,
, ,求(1)
,求(1) 的面积;(2)
的面积;(2) 的值.
的值. 
如图,矩形 的边
的边 在
在 的边
的边 上,顶点
上,顶点 、
、 分别在边
分别在边 、
、 上,
上, ,垂足为
,垂足为 .已知
.已知 ,
, .
.
(1)当矩形 为正方形时,求该正方形的边长;
为正方形时,求该正方形的边长;
(2)当矩形 面积为18时,求矩形的长和宽.
面积为18时,求矩形的长和宽.
如图,点D、E分别在△ABC的边AB、AC上,DE∥BC.
(1)若 ,
, ,求
,求 ;
;
(2)若 ,
, ,求
,求 (用m、n表示).
(用m、n表示).
如图,已知 ,AB的中垂线
,AB的中垂线 交
交 于点
于点 ,交
,交 于点
于点 ,
,  平分
平分 .
.
(1)求证: ∽
∽ ;
;
(2)求 的值;
的值;
(3)求 的值;
的值;
如图,已知△ 中,
中, ,
, ,
, ,把线段
,把线段 沿射线
沿射线 方向平移至PQ,直线PQ与直线AC交于点E,又联结BQ与直线AC交于点D.
方向平移至PQ,直线PQ与直线AC交于点E,又联结BQ与直线AC交于点D.
(1)若 ,求
,求 的长;
的长;
(2)设 ,
, ,试求y关于x的函数解析式;
,试求y关于x的函数解析式;
(3)当 为多少时,以Q、D、E为顶点的三角形与
为多少时,以Q、D、E为顶点的三角形与 相似.
相似.