下列各组值①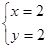 ②
②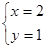 ③
③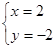 ④
④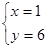 是方程
是方程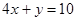 的解有( )
的解有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若方程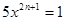 是一元一次方程,则
是一元一次方程,则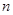 等于( )
等于( )
A.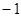 |
B. |
C.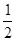 |
D.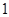 |
下列等式变形正确的是:( )
A.如果 ,那么 ,那么 |
B.如果 ,则 ,则 |
C.如果 ,那么 ,那么 |
D.如果 ,那么 ,那么 |
甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )
| A.1℃~3℃ | B.3℃~5℃ |
| C.5℃~8℃ | D.1℃~8℃ |
解方程 ,去分母,得( )
,去分母,得( )
A. |
B. |
C. |
D. |
如图,天平右盘中的每个砝码的质量都是1g则物体A的质量 mg 的取值范围,在数轴上表示为( )
已知 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的值为( ).
的值为( ).
| A.1 | B.-1 | C. 2 | D.3 |
不等式组 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
若关于x、y的方程组 的解满足方程2x+3y=6,那么k的值为( )
的解满足方程2x+3y=6,那么k的值为( )
A.- |
B.- |
C. |
D. |
某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应按排几天精加工,几天粗加工?设安排 天精加工,
天精加工, 天粗加工.为解决这个问题,所列方程组正确的是( )
天粗加工.为解决这个问题,所列方程组正确的是( )
A. |
B. |
C. |
D. |
如图是正方体的表面展开图,标注了字母 的面是正方体的正面。若正方体相对的两个面上的数字相等,则
的面是正方体的正面。若正方体相对的两个面上的数字相等,则 和
和 的值分别是:( )
的值分别是:( )
A. , , |
B. , , |
C. , , |
D. , , |
若关于 的不等式
的不等式 的整数解共有4个,则
的整数解共有4个,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
不等式 的所有正整数解之和为: 。
的所有正整数解之和为: 。
已知 ,
, ,则
,则 。
。
已知代数式 与
与 互为相反数,那么
互为相反数,那么 = 。
= 。
关于 的方程
的方程 的解为正实数,则
的解为正实数,则 的取值范围是 。
的取值范围是 。
初三的几位同学拍了一张合影作留念,已知冲一张底片需要0.80元,洗一张相片需要0.35元。在每位同学得到一张相片、共用一张底片的前提下,平均每人分摊的钱不足0.5元,那么参加合影的同学人数至少为 人。
若 ,则
,则 。
。
解方程: 
解不等式,并将解集表示在数轴上。
解方程组:
一项工程,甲单独做15天完成,乙单独做20天完成。若乙先单独做6天后,甲再加入合作,问:共需要多少天完成此项工程?
已知 是负整数,且
是负整数,且 ,求代数式
,求代数式 的值。
的值。
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示。根据图中的数据(单位:m),解答下列问题:
⑴用含 、
、 的代数式表示地面总面积;
的代数式表示地面总面积;
⑵已知客厅面积比卫生间面积多21m2,且地面总面积是卫生间面积的15倍。若铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
万物皆有规律,请你找一找下面方程组中隐含的规律。
⑴解方程组:
⑵猜测并解方程组 的解为: 。
的解为: 。
⑶请写出一个具有你发现规律的方程组 。
小赵为班级购买笔记本作为晚会上的奖品。回来时向生活委员交账说:“一共买了36本,有两种规格,单价分别为1.8元和2.6元。去时我领了100元,现在找回27.6元。”生活委员算了一下,认为小赵搞错了。
⑴请你用方程的知识说明小赵为什么搞错了。
⑵小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起当做找回的钱给了生活委员。如果设购买单价为1.8元的笔记本 本,试用含
本,试用含 的代数式表示小赵零用钱的数目:
的代数式表示小赵零用钱的数目:
元。
⑶如果小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目。