已知复数 ,那么
,那么 对应的点位于复平面内的
对应的点位于复平面内的
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
已知集合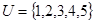 ,
, ,
,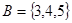 ,则
,则
A.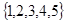 |
B.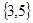 |
C. |
D. |
为了得到函数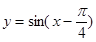 的图象,只需把函数
的图象,只需把函数 的图象
的图象
A.向右平移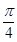 个长度单位 个长度单位 |
B.向左平移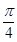 个长度单位 个长度单位 |
C.向右平移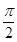 个长度单位 个长度单位 |
D.向左平移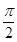 个长度单位 个长度单位 |
用反证法证明“方程 至多有两个解”的假设中,正确的是
至多有两个解”的假设中,正确的是
| A.至多有一个解 | B.有且只有两个解 |
| C.至少有三个解 | D.至少有两个解 |
曲线 在点
在点 处的切线方程为
处的切线方程为
A. |
B. |
C. |
D. |
某人进行了如下的“三段论”推理:
如果 ,则
,则 是函数
是函数 的极值点,因为函数
的极值点,因为函数 在
在 处的导数值
处的导数值 ,所以,
,所以, 是函数
是函数 的极值点。你认为以上推理的
的极值点。你认为以上推理的
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
函数 的单调递减区间是
的单调递减区间是
A. |
B. |
C. |
D. |
在 中,
中, ,则此三角形解的个数为
,则此三角形解的个数为
| A.0 | B.1 | C.2 | D.无数个 |
下列函数在区间(1,2)上有零点的是
A.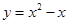 |
B.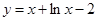 |
C. |
D. |
函数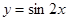 的图象与函数
的图象与函数 的图象在开区间
的图象在开区间 上的一种较准确的判断是
上的一种较准确的判断是
| A.至少有两个交点 | B.至多有两个交点 |
| C.至多有一个交点 | D.至少有一个交点 |
函数 的导函数
的导函数 的图象大致是
的图象大致是
设偶函数 满足
满足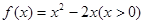 ,则
,则
A.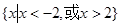 |
B.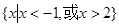 |
C. |
D. |
已知函数 ,或
,或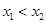 ,且
,且 ,则
,则
A.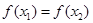 |
B. |
C.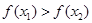 |
D.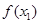 与 与 的大小不能确定 的大小不能确定 |
函数 图象上关于坐标原点O对称的点恰有5对,则
图象上关于坐标原点O对称的点恰有5对,则 的值可以为
的值可以为
A. |
B. |
C. |
D. |
已知函数 则
则 。
。
若复数 为纯虚数,则t的值为 。
为纯虚数,则t的值为 。
若 ,则
,则 。
。
程序框图如下图所示,若 ,输入
,输入 ,则输出结果为 。
,则输出结果为 。
已知点 是函数
是函数 的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论
的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论 成立。运用类比思想方法可知,若点
成立。运用类比思想方法可知,若点 ,
, 是函数
是函数 的图象上的不同两点,则类似地有成立 。
的图象上的不同两点,则类似地有成立 。
如图,线段AB=6,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D。设CP=x, CPD的面积为
CPD的面积为 ,则
,则 的最大值为 。
的最大值为 。
已知 ,且
,且
 。求
。求 的值。
的值。
已知复数 ,且
,且 。
。
(Ⅰ)若 时,且
时,且 ,求x的值;
,求x的值;
(Ⅱ)设 ,求
,求 的单调递增区间。
的单调递增区间。
在锐角 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是 ,且
,且 。
。
(Ⅰ)求B;
(Ⅱ)若 ,求周长
,求周长 的最大值。
的最大值。
已知函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为 。
。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若关于x的方程 在区间
在区间 上恰有两个相异实根,求m的取值范围。
上恰有两个相异实根,求m的取值范围。
已知函数 。
。
(Ⅰ)若当 时,
时, 的最小值为-1,求实数k的值;
的最小值为-1,求实数k的值;
(Ⅱ)若对任意的 ,均存在以
,均存在以 为三边边长的三角形,求实数k的取值范围。
为三边边长的三角形,求实数k的取值范围。