已知集合 ,
,
则 为( )
为( )
A. |
B. |
C. |
D. |
若 ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A. |
B. |
C. |
D. |
在等差数列{an}中,已知a4+a8=16,则a2+a10=( )
| A.12 | B.16 | C.20 | D.24 |
若 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )
| A.7 | B.5 | C.-5 | D.-7 |
函数 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A. |
B.0 | C.-1 | D. |
下列判断正确的是( )
A.若命题 为真命题,命题 为真命题,命题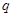 为假命题,则命题“ 为假命题,则命题“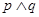 ”为真命题 ”为真命题 |
B.命题“若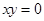 ,则 ,则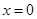 ”的否命题为“若 ”的否命题为“若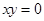 ,则 ,则 ” ” |
C.“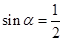 ”是“ ”是“  ”的充分不必要条件 ”的充分不必要条件 |
D.命题“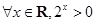 ”的否定是“ ”的否定是“  ” ” |
函数 的零点个数为( )
的零点个数为( )
| A.2 | B.3 | C.4 | D.5 |
函数 (其中
(其中 )的图象如图1所示,为了得到
)的图象如图1所示,为了得到 的图象,则只需将
的图象,则只需将 的图象( )
的图象( )
A.向右平移 个长度单位 个长度单位 |
B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |
已知函数 则满足不等式
则满足不等式 的
的 的取值范围为( )
的取值范围为( )
A. |
B.(-3,1) | C.[-3,0) | D.(-3,0) |
设不等式组 表示的平面区域为
表示的平面区域为 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则 =( )
=( )
| A.1012 | B.2012 | C.3021 | D.4001 |
已知向量a,b夹角为 ,且|a|=1,|2a-b|=
,且|a|=1,|2a-b|= ,则|b|=________.
,则|b|=________.
在△ 中,
中, ,
, ,则
,则 的长度为________.
的长度为________.
设 满足约束条件:
满足约束条件: 则
则 的取值范围为 .
的取值范围为 .
已知 ,若
,若 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
已知函数 。
。
(1)求 的定义域及最小正周期;
的定义域及最小正周期;
(2)求 的单调递减区间.
的单调递减区间.
已知公差不为零的等差数列 满足
满足 ,且
,且 成等比数列。
成等比数列。
(1)求数列 的通项公式
的通项公式 ;
;
(2)设 为数列
为数列 的前n项和,求数列
的前n项和,求数列 的前n项和
的前n项和
已知a,b,c分别为△ABC三个内角A,B,C的对边,c =  asinC-ccosA.
asinC-ccosA.
(1)求A;
(2)若a=2,△ABC.的面积为 ,求b,c.
,求b,c.
已知等差数列 满足:
满足: .
.
(1)求 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前n项和
的前n项和 .
.
如图2,建立平面直角坐标系 ,
, 轴在地平面上,
轴在地平面上, 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程 表示的曲线上,其中
表示的曲线上,其中 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
设f(x)=lnx+ -1,证明:
-1,证明:
(1)当x>1时,f(x)< (x-1);
(x-1);
(2)当1<x<3时,f(x)< .
.