设集合 则A∩B= ( )
则A∩B= ( )
| A.ø | B.(3.4) | C.(-2.1) | D.(4.+∞) |
已知函数 集合A∩B只含有一个元素,则实数t的取值范围是 ( )
集合A∩B只含有一个元素,则实数t的取值范围是 ( )
A. |
B. |
C. |
D. |
命题“若a>b,则a+1>b”的逆否命题是 ( )
| A.若a+1≤b则a>b | B.若a+1<b则a>b |
| C.若a+1≤b则a≤b | D.若a+1<b则a<b |
.设x.y是两个实数,命题“x,y中至少有一个大于1”成立的充分不必要条件是 ( )
| A.x+y=2 | B.x+y>2 |
C. |
D.xy>1 |
已知sinx="2cosx" 则 sin ( )
( )
A. |
B. |
C. |
D. |
在△ABC中,a.b.c分别是角A.B.C的对边,若a-b= 则边C的值为 ( )
则边C的值为 ( )
A.1 B.  C.2 D.
C.2 D. 
已知平面上不共线的四点O.A.B.C,若 则
则 ( )
( )
A.  B.
B.  C.3 D.2
C.3 D.2
函数 在定义域R内可导,若
在定义域R内可导,若 ,且当
,且当 时,
时, ,设a=f(0).b=
,设a=f(0).b= 则 ( )
则 ( )
| A.a<b<c | B.c<b<a | C.c<a<b | D.b<c<a |
已知 ,记
,记
则 ( )
( )
| A.-1 | B.0 | C. |
D.1 |
计算: _____________
_____________
若函数 的图象关于直线x=-1对称,则实数a的值是___________
的图象关于直线x=-1对称,则实数a的值是___________
复数 在复平面内对应的点到原点的距离为_____________________
在复平面内对应的点到原点的距离为_____________________
函数 的图象为C,如下 结论中正确的是_______________(写出所有正确结论的序号)①图象C关于直线
的图象为C,如下 结论中正确的是_______________(写出所有正确结论的序号)①图象C关于直线 对称②图象C关于点
对称②图象C关于点 对称③函数
对称③函数 在区间
在区间 内是增函数④由
内是增函数④由 的图象向右平移
的图象向右平移 个单位可以得到图象C
个单位可以得到图象C
若命题“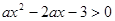 不成立”是真命题,则实数a的取值范围是__________
不成立”是真命题,则实数a的取值范围是__________
如图,函数 的图象是曲线OAB,其中O.A.B的坐标分别是(0,0),(1,2),(3,1)则
的图象是曲线OAB,其中O.A.B的坐标分别是(0,0),(1,2),(3,1)则 的值为_____________________________
的值为_____________________________
 是连续的偶函数,且当x>o时,
是连续的偶函数,且当x>o时, 是单调函数,则满足
是单调函数,则满足 的所有x为之和______________________________
的所有x为之和______________________________
已知函数 的最大值是1,其图象经过点M
的最大值是1,其图象经过点M
(1)求 的解析式(2)已知
的解析式(2)已知 且
且 求
求 的值。
的值。
命题P:实数x满足 其中a<0,命题q:实数x满足
其中a<0,命题q:实数x满足 或
或 且
且 是
是 的必要不充分条件,求a的取值范围
的必要不充分条件,求a的取值范围
在△ABC中,a.b.c分别为内角A.B.C所对的边,且满足
(1)求角A的大小
(2)现给出三个条件:①a=2.②B=45°③C= 试从中选出两个可以确定△ABC的条件写出你的
试从中选出两个可以确定△ABC的条件写出你的
选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记
分)
抛物线 上有两点
上有两点 且
且 (0为坐标原点)
(0为坐标原点)
(1)求证: ∥
∥ (2)若
(2)若 ,求AB所在直线方程。
,求AB所在直线方程。
某企业拟在2012年度进行一系列促销活动,已知某产品年销量x万件与年促销费用t万元之间满足3-x与t+1成反比例,当年促销费用t=0万元时,年销量是1万件,已知2012年产品的设备折旧、维修等固定费用为3万元,每生产1万件产品需再投入32万元的生产费用。若将每件产品售价定为:其生产成本的150%与“平均每件促销费的一半”之和,则当年生产的商
(1)将2012年的利润y(万元)表示为促销费t(万元)的函数
(2)该企业2012年的促销费投入多少万元时,企业年利润最大?(注:利润=销售收入-生产成
本-促销费,生产成本=固定费用+生产费用)
已知
(1)求函数 在[t,t+2](t>0)上的最小值
在[t,t+2](t>0)上的最小值
(2)对一切 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。