已知全集 ,集合
,集合 ,集合
,集合 则
则 等于 ( )
等于 ( )
A. |
B. |
C. |
D. |
下列对应法则 中,可以构成从集合
中,可以构成从集合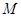 到集合
到集合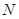 的映射的是( )
的映射的是( )
A.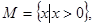 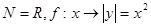 |
B.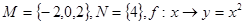 |
C.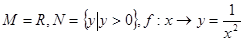 |
D.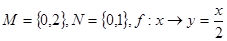 |
下列各组函数中表示同一函数的是 ( )
① 与
与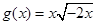 ;②
;②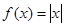 与
与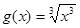 ;
;
③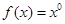 与
与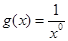 ;④
;④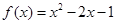 与
与 .
.
| A.①② | B.②③ | C.③④ | D.①④ |
集合
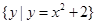 ,则阴影部分表示的集合为( )
,则阴影部分表示的集合为( )
A.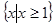 |
B. |
C.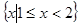 |
D.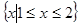 |

设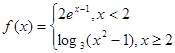 ,则
,则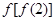 的值为( )
的值为( )
| A.0 | B.1 | C.2 | D.2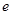 |
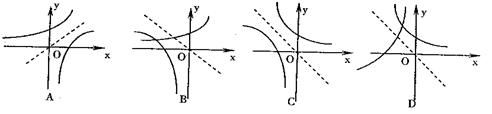
已知 ,函数
,函数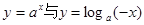 的图象只可能是( )
的图象只可能是( )
设 ,则
,则 的大小关系为( )
的大小关系为( )
A. |
B. |
C. |
D. |
若函数 与
与 在区间
在区间 上都是减函数,则实数
上都是减函数,则实数 的取值范围是( )
的取值范围是( )
A. ∪ ∪ |
B. ∪ ∪ |
C. |
D. |
若 ( )
( )
A. |
B. |
C. |
D. |
若定义运算 ,则函数
,则函数 的值域是( )
的值域是( )
A. |
B. |
C. |
D. |
已知偶函数 在区间
在区间 上单调递增,则满足不等式
上单调递增,则满足不等式 的
的 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
若函数 是
是 上的减函数,则实数
上的减函数,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
求函数 的定义域 ;
的定义域 ;
计算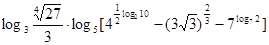 = ;
= ;
函数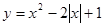 的单调增区间为 ;
的单调增区间为 ;
里氏震级 的计算公式为:
的计算公式为: 其中
其中 是测震仪记录的地震曲线的最大振幅,
是测震仪记录的地震曲线的最大振幅, 为“标准地震”的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则此次地震的震级为__________级;9级地震的最大振幅是5级地震的最大振幅的__________倍.
为“标准地震”的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则此次地震的震级为__________级;9级地震的最大振幅是5级地震的最大振幅的__________倍.
已知集合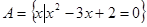 ,
,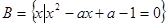 ,若
,若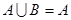 ,求实数
,求实数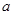 的值.
的值.
已知函数
(1)当 时,求函数的最大值与最小值;
时,求函数的最大值与最小值;
(2)求实数 的取值范围,使得
的取值范围,使得 在区间
在区间 上是单调函数.
上是单调函数.
某公司要将一批不易存放的蔬菜从 地运到
地运到 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 |
途中速度 (千米/小时) |
途中单位费用(元/千米) |
装卸时间 (小时) |
装卸费用(元) |
| 汽车 |
50 |
8 |
2 |
1000 |
| 火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程中(含装卸时间)损耗为300元/小时,设 、
、 两地距离为
两地距离为 千米.
千米.
(1)设采用汽车与火车运输的总费用分别为 与
与 ,求
,求 与
与 的解析式;
的解析式;
(2)试根据 、
、 两地距离的大小比较采用哪种运输工具更合算(即运输总费用最小).(注:总费用=途中费用+装卸费用+损耗费用)
两地距离的大小比较采用哪种运输工具更合算(即运输总费用最小).(注:总费用=途中费用+装卸费用+损耗费用)
已知 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, ;
;
(1)求 在
在 上的解析式;
上的解析式;
(2)试判断函数 在区间
在区间 上的单调性,并给出证明.
上的单调性,并给出证明.
已知函数 的定义域为
的定义域为 ,对于任意的
,对于任意的 ,都有
,都有 ,且当
,且当 时,
时, ,若
,若 .
.
(1)求证: 为奇函数;
为奇函数;
(2)求证: 是
是 上的减函数;
上的减函数;
(3)求函数 在区间
在区间 上的值域.
上的值域.
已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性并证明你的结论;
的奇偶性并证明你的结论;
(3)试讨论 的单调性.
的单调性.