若
，则下列不等式①
；②
；③
；④
中，正确的不等式有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
已知命题
关于
的方程
有实根，命题
关于函数
在
上为增函数，若“
或
”为真命题，“且”为假命题，则实数
取值范围为（ ）
A． |
B． |
C． |
D． |
已知函数
，
，则函数
的振幅为（ ）
A． |
B． |
C． |
D． |
已知等差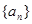数列
与等比数列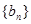
各项都是正数，且
，
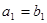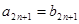，那么一定有（ ）
A． |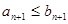
B． |
C． |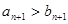
D． |
定义在
上的函数
，则
的图像与直线
的交点为
、
、
且
，则下列说法错误的是（ ）
A． |
B． |
C． |
D． |
已知点
在不等式组
确定的平面区域内，则点
所在平面区域的面积是（ ）
A． |
B． |
C． |
D． |
等差数列
中，
，
是方程
的两个根，则数列
前
项和
（ ）
A． |
B． |
C． |
D． |
已知圆
与直线
及
都相切，圆心在直线
上，则圆的方程为（ ）
A． |
B． |
C． |
D． |
已知向量
，并且满足关系：
,则
的最大值为 ( )
A． |
B． |
C． |
D． |
已知函数
则
的图象是 ( )
| A． | B． | C． | D． |
设向量
满足：
．以
的模为边长构成三角形，则它的边与半径为
的圆的公共点个数最多为 ( )
A． |
B． |
C． |
D． |
已知函数
，且函数
在区间（0，1）内取得极大值，在区间（1，2）内取得极小值，则
的取值范围为( )
A． |
B． |
C． |
D． |
中，
，三角形面积为
，则
的值为 .
若⊙
与⊙
相交于
两点，且两圆在点
处的切线互相垂直，则线段
的长度是 
已知曲线
的切线
过点
，则切线的斜率为______.
设
为
的内心，当
时，
，则
的值为________.
（本小题满分10分）
已知
是
的三个内角，若向量
，
，且
。
（1）求证：
； （2）求
的最大值。
（本小题满分12分）
已知定义域为
的函数
是奇函数．
（1）求
的值；
（2）若对任意的
，不等式
恒成立，求
的取值范围.
（本小题满分12分）
等比数列{
}的前
项和为
，已知对任意的
，点
均在函数
且
均为常数)的图像上.
（1）求
的值；
（2）当
时，记
，求数列
的前项和
.
（本小题满分12分）
设平面直角坐标系
中，设二次函数
的图象与两坐标轴有三个交点，经过这三个交点的圆记为
．求：
（Ⅰ）求实数
的取值范围；
（Ⅱ）求圆的方程；
（Ⅲ）问圆是否经过某定点（其坐标与b 无关）？请证明你的结论．
（本小题满分12分）
已知
，解不等式
（本小题满分12分）
已知函数
在
上是增函数，在
上是减函数．
（1）求函数
的解析式；
（2）若
时，
恒成立，求实数
的取值范围；
（3）是否存在实数
，使得方程
在区间
上恰有两个相异实数根，若存在，求出的范围，若不存在说明理由．