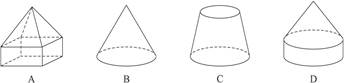
如图是一个物体的三视图,则此三视图所描述的物体是下列几何体中的( )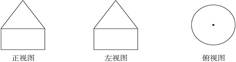
圆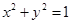 和圆
和圆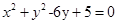 的位置关系是( )
的位置关系是( )
| A.外切 | B.内切 | C.外离 | D.内含 |
下列叙述中错误的是( )
A.若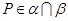 且 且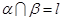 ,则 ,则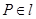 ; ; |
B.三点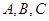 确定一个平面; 确定一个平面; |
C.若直线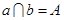 ,则直线 ,则直线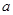 与 与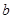 能够确定一个平面; 能够确定一个平面; |
D.若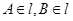 且 且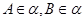 ,则 ,则 . . |
如果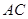 <0,
<0,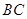 <0,那么直线
<0,那么直线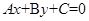 不通过( )
不通过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
平行六面体 中,设
中,设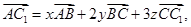 则
则 ( )
( )
| A.1 | B.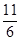 |
C.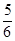 |
D.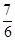 |
在空间四边形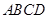 中,
中,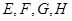 分别是
分别是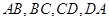 的中点。若
的中点。若 ,且
,且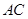 与
与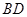 所成的角为
所成的角为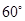 ,则四边形
,则四边形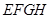 的面积为( )
的面积为( )
A. |
B.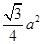 |
C.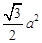 |
D.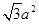 |
已知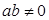 ,点
,点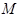
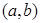 是圆
是圆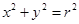 内一点,直线
内一点,直线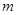 是以点
是以点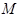 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线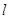 的方程是
的方程是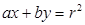 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.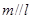 ,且 ,且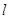 与圆相交 与圆相交 |
B.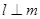 ,且 ,且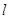 与圆相切 与圆相切 |
C.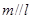 ,且 ,且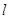 与圆相离 与圆相离 |
D.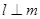 ,且 ,且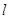 与圆相离 与圆相离 |
将边长为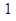 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,在折起后形成的三棱锥
,在折起后形成的三棱锥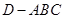 中,给出下列三个命题:
中,给出下列三个命题:
①面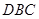 是等边三角形; ②
是等边三角形; ②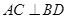 ; ③三棱锥
; ③三棱锥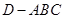 的体积是
的体积是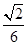 .
.
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
若直线 与曲线
与曲线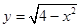 有两个交点,则
有两个交点,则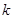 的取值范围是( )
的取值范围是( )
A.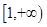 |
B.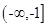 |
C.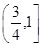 |
D.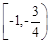 |
已知平面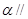 平面
平面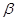 ,
,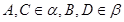 ,线段
,线段 与线段
与线段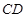 交于点
交于点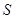 ,若
,若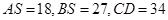 ,则
,则 = ( )
= ( )
A. |
B.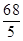 |
C.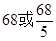 |
D.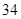 |
直线 截圆
截圆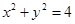 得到的弦长为 .
得到的弦长为 .
一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为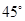 ,腰和上底均为1(如图),则平面图形的实际面积为 .
,腰和上底均为1(如图),则平面图形的实际面积为 .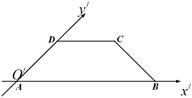
已知点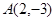 、
、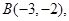 直线
直线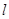 过点
过点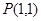 ,且与线段
,且与线段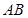 相交,则直线
相交,则直线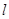 的斜率
的斜率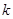 的取值范围是 .
的取值范围是 .
长方体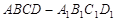 中,
中, ,则从
,则从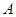 点沿表面到
点沿表面到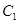 点的最短距离为 .
点的最短距离为 .
正四棱锥 的侧棱长为
的侧棱长为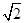 ,底面边长为
,底面边长为 ,
,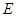 为
为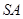 中点,则异面直线
中点,则异面直线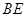 与
与 所成的角是 .
所成的角是 .
若圆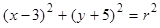 上有且只有两个点到直线
上有且只有两个点到直线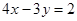 的距离为1,则半径
的距离为1,则半径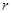 的取值范围是 .
的取值范围是 .
已知两条不同直线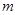 、
、 ,两个不同平面
,两个不同平面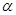 、
、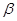 ,给出下列命题:
,给出下列命题:
(1)若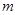

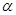 ,
,

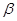 且
且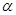 ∥
∥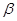 ,则
,则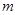 ∥
∥ ;(2)若
;(2)若

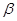 ,
,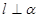 ,则
,则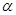 ⊥
⊥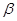 ;
;
(3)若 ∥
∥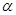 ,则
,则 平行于
平行于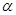 内的所有直线;(4)若
内的所有直线;(4)若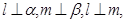 则
则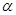 ⊥
⊥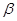 ;
;
(5)若 在平面
在平面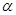 内的射影互相垂直,则
内的射影互相垂直,则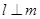 。
。
其中正确命题的序号是 (把你认为正确命题的序号都填上).
(本小题满分8分)已知直线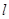 经过点
经过点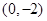 ,且垂直于直线
,且垂直于直线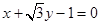 ,
,
(1)求直线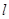 的方程;(2)求直线
的方程;(2)求直线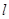 与两坐标轴围成三角形的面积。
与两坐标轴围成三角形的面积。
(本小题满分8分)如图四边形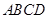 为梯形,
为梯形,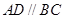 ,
,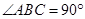 ,求图中阴影部分绕
,求图中阴影部分绕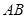 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。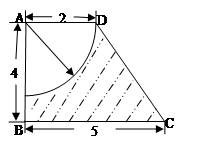
(本小题满分12分) 如图,在四棱锥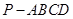 中,底面
中,底面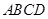 是正方形,侧棱
是正方形,侧棱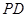 ⊥底面
⊥底面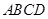 ,
,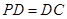 ,
, 是
是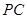 的中点,作
的中点,作 交
交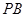 于点
于点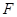
(1) 证明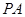 //平面
//平面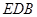 ;
;
(2) 证明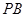 ⊥平面
⊥平面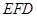 ;
;
(3) 求二面角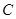 —
—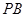 —
—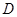 的大小。
的大小。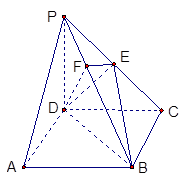
(本小题满分12分)已知圆 以
以 为圆心且经过原点O.
为圆心且经过原点O.
(1) 若直线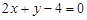 与圆
与圆 交于点
交于点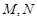 ,若
,若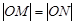 ,求圆
,求圆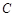 的方程;
的方程;
(2) 在(1)的条件下,已知点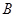 的坐标为
的坐标为 ,设
,设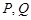 分别是直线
分别是直线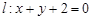 和圆
和圆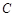 上的动点,求
上的动点,求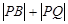 的最小值及此时点
的最小值及此时点 的坐标。
的坐标。
(本小题满分12分)如图,三棱柱 的各棱长均为2,侧面
的各棱长均为2,侧面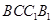
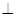 底面
底面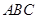 ,侧棱
,侧棱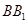 与底面
与底面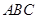 所成的角为
所成的角为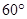 .
.
(1) 求直线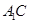 与底面
与底面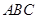 所成的角;
所成的角;
(2) 在线段 上是否存在点
上是否存在点 ,使得平面
,使得平面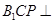 平面
平面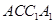 ?若存在,求出
?若存在,求出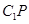 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。