若集合 ,则
,则 =( )
=( )
| A.{4} | B.{1,2,3,4,5} |
C. |
D. |
已知 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A. |
B. |
C. |
D. |
已知 为等差数列,若
为等差数列,若 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
已知 .下列四个条件中,使
.下列四个条件中,使 成立的必要而不充分的条件是( )
成立的必要而不充分的条件是( )
A. |
B. |
C. |
D. |
某几何体的三视图及尺寸如图示,则该几何体的表面积为( )
A. |
B. |
C. |
D.  |
若双曲线 的渐近线方程为
的渐近线方程为 则双曲线的一个焦点F到渐近线的距离为( )
则双曲线的一个焦点F到渐近线的距离为( )
| A.2 | B. |
C. |
D. |
已知 是实数,则函数
是实数,则函数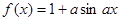 的图象不可能是( )
的图象不可能是( )
在△ABC中,a、b、c分别为三个内角A、B、C所对的边,设向量
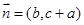 ,若
,若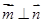 ,则角A的大小为( )
,则角A的大小为( )
A.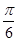 B.
B.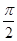 C.
C.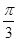 D.
D.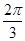
O为ΔABC的内切圆圆心,且AB=5,BC=4,CA=3,下列结论中正确的是( )
A. |
B. > >  |
C. = = = = |
D. < < = = |
函数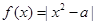 在区间
在区间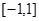 上的最大值
上的最大值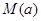 的最小值是( )
的最小值是( )
A.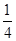 |
B.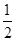 |
C.1 | D.2 |
若变量 满足约束条件
满足约束条件 ,则
,则 的最大值为 .
的最大值为 .
已知点 在直线
在直线 上,则
上,则 的最小值为 .
的最小值为 .
过点 的直线
的直线 将圆
将圆 截成两段弧,若其中劣弧的长度最短,那么直线
截成两段弧,若其中劣弧的长度最短,那么直线 的方程为 。
的方程为 。
一个四面体所有棱长都为 ,四个顶点在同一球面上,则此球表面积为 。
,四个顶点在同一球面上,则此球表面积为 。
对于函数 ,若存在区间
,若存在区间 ,当
,当 时的值域为
时的值域为
 ,则称
,则称 为
为 倍值函数.若
倍值函数.若 是
是 倍值函数,则实数
倍值函数,则实数 的取值范围是 。
的取值范围是 。
(本小题满分13分)
如图,在平面直角坐标系中,锐角 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点.
(Ⅰ)如果 ,点
,点 的横坐标为
的横坐标为 ,求
,求 的值;
的值;
(Ⅱ)已知点
 ,求函数
,求函数 的值域.
的值域.
(本小题满分13分)
已知数列 满足:
满足: ,其中
,其中 为数列
为数列 的前
的前 项和.
项和.
(Ⅰ)试求 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: ,试求
,试求 的前
的前 项和公式
项和公式 .
.
(本小题满分13分)
直线y=kx+b与曲线 交于A、B两点,记△AOB的面积为S(O是坐标原点)。
交于A、B两点,记△AOB的面积为S(O是坐标原点)。
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(本小题满分13分)
如图,  是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)设点 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论.
(本小题满分14分) 已知函数 ,其中
,其中 。
。 。
。
(1)若 是函数
是函数 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若函数 的图象上任意一点处切线的斜率
的图象上任意一点处切线的斜率 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数 在
在 上有两个零点,求实数a的取值范围。
上有两个零点,求实数a的取值范围。
(本小题满分14分)
选修4-2:矩阵及其变换
(1)如图,向量 被矩阵M作用后分别变成
被矩阵M作用后分别变成 ,
,
(Ⅰ)求矩阵M;
(Ⅱ)并求 在M作用后的函数解析式;
在M作用后的函数解析式;
选修4-4:坐标系与参数方程
( 2)在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为 。
。
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设圆 与直线
与直线 交于点
交于点 。若点
。若点 的坐标为(3,
的坐标为(3, ),求
),求 。
。
选修4-5:不等式选讲
(3)已知 为正实数,且
为正实数,且 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.