设复数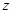 满足
满足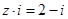 ,
,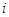 为虚数单位,则
为虚数单位,则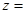 ( )
( )
A.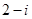 |
B.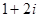 |
C.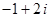 |
D. |
设f(x)=3x-x2,则在下列区间中,使函数f(x)有零点的区间是( )
| A.(0,1) | B.(1,2) | C.(-2,-1) | D.(-1,0) |
集合 ,
,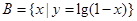 ,则
,则 等于 ( )
等于 ( )
A.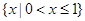 |
B.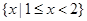 |
C.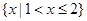 |
D.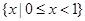 |
已知向量 满足
满足 ,则
,则 与
与 的夹角为 ( )
的夹角为 ( )
A. |
B. |
C. |
D. |
已知等差数列 满足
满足 ,
, ,
, ,则
,则 的值为
的值为
A. |
B. |
C. |
D. |
已知 是三角形
是三角形 的内角,则“
的内角,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 ,且
,且 ,则
,则 ,
, ,
, ,则这三个数的大小关系为( )
,则这三个数的大小关系为( )
| A.P<N<M | B.N<P<M | C.N<M<P | D.P<M<N |
已知 ,
, ,
, 为三条不同的直线,
为三条不同的直线, ,
, 为两个不同的平面,则下列命题中正确的是( )
为两个不同的平面,则下列命题中正确的是( )
A. |
B. ∥ ∥ |
C. |
D. ∥ ∥ |
某同学设计右面的程序框图用以计算和式 的值,则在判断框中应填写
的值,则在判断框中应填写
A. |
B. |
C. |
D. |
若变量 满足约束条件
满足约束条件 ,则
,则 的最大值为
的最大值为
A. |
B. |
C. |
D. |
已知函数 ,则使方程
,则使方程 有解的实数m的取值范围是( )
有解的实数m的取值范围是( )
| A.(1,2) | B. |
C. |
D. |
椭圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 则点
则点 位置( )
位置( )
A.必在圆 内 内 |
B.必在圆 上 上 |
C.必在圆 外 外 |
D.以上三种情况都有可能 |
已知函数 的导函数为偶函数,则
的导函数为偶函数,则 .
.
圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为______.
一个空间几何体的三视图(单位: )如图所示,则该几何体的体积为_______
)如图所示,则该几何体的体积为_______ .
. 
记 当
当 时,
时,
观察下列等式: ,
,  ,
, ,
, ,
, ,
,
可以推测, .
.
(本小题满分12分)已知函数
 。
。
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的单调递增区间,并写出对称轴方程.
的单调递增区间,并写出对称轴方程.
(本小题满分12分)已知等比数列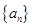 满足
满足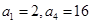 。
。
(1)求数列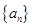 的通项公式;
的通项公式;
(2)设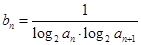 ,
,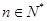 ,求数列
,求数列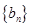 的前
的前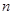 项和
项和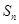 。
。
(本小题满分12分)在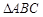 中,设内角A,B,C的对边分别为
中,设内角A,B,C的对边分别为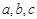 ,向量
,向量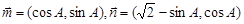 ,若
,若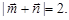
(1)求角的大小;
(2)若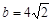 且
且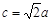 ,求
,求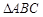 的面积.
的面积.
(本小题满分12分)在几何体ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
(Ⅰ)求证:DC∥平面ABE;
(Ⅱ)求证:AF⊥平面BCDE;
(Ⅲ)求证:平面AFD⊥平面AFE.
(本小题满分12分) 已知椭圆 的焦距为
的焦距为 ,椭圆
,椭圆 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线
 与椭圆
与椭圆 交于
交于 两点,点
两点,点 (0,1),且
(0,1),且 =
= ,求直线
,求直线 的方程.
的方程.
(本小题满分14分)已知函数
(1)求函数 的极值点;
的极值点;
(2)若直线 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线 相切,求直线
相切,求直线 的方程;
的方程;
(3)设函数 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数
上的最小值.(其中e为自然对数的底数