若集合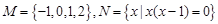 ,则
,则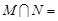
A.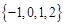 |
B.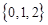 |
C.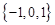 |
D.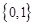 |
点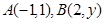 ,向量
,向量 ,若
,若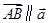 ,则实数
,则实数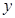 的值为
的值为
| A.5 | B.6 | C.7 | D.8 |
三个数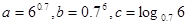 之间的大小关系是
之间的大小关系是
A.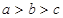 |
B.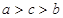 |
C.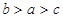 |
D.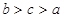 |
由表格中的数据可以判定方程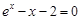 的一个零点所在的区间是
的一个零点所在的区间是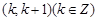 ,则
,则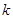 的值为
的值为
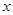 |
-1 |
0 |
1 |
2 |
3 |
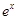 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
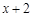 |
1 |
2 |
3 |
4 |
5 |
A. -1 B.0 C.1 D.2
若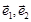 是夹角为
是夹角为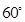 的两个单位向量,则
的两个单位向量,则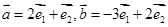 的夹角为
的夹角为
A.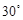 |
B.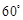 |
C. |
D.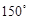 |
为了得到函数 的图像,需要把函数
的图像,需要把函数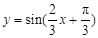 图像上的所有点
图像上的所有点
A.横坐标缩短到原来的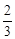 倍,再向右平移 倍,再向右平移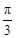 个单位长度 个单位长度 |
B.横坐标伸长到原来的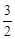 倍,再向右平移 倍,再向右平移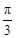 个单位长度 个单位长度 |
C.横坐标缩短到原来的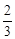 倍,再向左平移 倍,再向左平移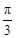 个单位长度 个单位长度 |
D.横坐标伸长到原来的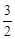 倍,再向左平移 倍,再向左平移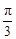 个单位长度 个单位长度 |
北京时间2012年10月11日19点,瑞典文学院诺贝尔奖评审委员会宣布,中国作家莫言获得2012年诺贝尔文学奖,全国反响强烈,在全国掀起了出书的热潮.国家对出书所得稿费纳税作如下规定:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14%纳税;超过4000元的按全稿酬的11%纳税.某人出版了一书共纳税420元,这个人的稿费为
| A.3000元 | B.3800元 | C.3818元 | D.5600元 |
已知两个非零向量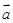 与
与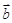 ,定义
,定义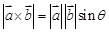 ,其中
,其中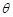 为
为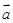 与
与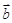 的夹角,若
的夹角,若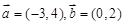 ,则
,则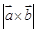 的值为
的值为
A.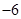 |
B.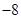 |
C.6 | D.8 |
函数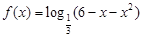 的单调递增区间是
的单调递增区间是
A. |
B.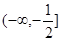 |
C.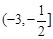 |
D.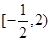 |
某学习小组对函数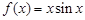 进行研究,得出了如下四个结论:①函数
进行研究,得出了如下四个结论:①函数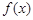 在
在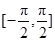 上单调递增;②存在常数
上单调递增;②存在常数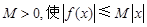 对一切实数
对一切实数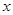 均成立;③函数
均成立;③函数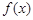 在
在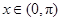 上无最小值,但一定有最大值;④点
上无最小值,但一定有最大值;④点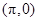 是函数
是函数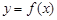 的一个对称中心,其中正确的是
的一个对称中心,其中正确的是
| A.①③ | B.②③ | C.②④ | D.①②④ |
幂函数 的图象过点
的图象过点 ,则
,则 .
.
已知函数 ,则
,则 .
.
一个扇形的面积是 ,它的周长是
,它的周长是 ,则圆心角的弧度数是 .
,则圆心角的弧度数是 .
已知函数 ,如果
,如果 ,则
,则 的取值范围是 .
的取值范围是 .
有下列叙述:
①集合 中只有四个元素;
中只有四个元素;
② 在其定义域内为增函数;
在其定义域内为增函数;
③已知 ,则角
,则角 的终边落在第四象限;
的终边落在第四象限;
④平面上有四个互异的点 ,且点
,且点 不共线,已知
不共线,已知 ,则△
,则△ 是等腰三角形;
是等腰三角形;
⑤若函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 .
.
其中所有正确叙述的序号是 .
计算:
(Ⅰ)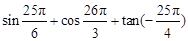
(Ⅱ)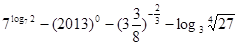
记函数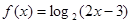 的定义域为集合
的定义域为集合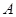 ,函数
,函数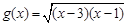 的定义域为集合
的定义域为集合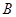 ,集合
,集合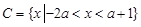 .
.
(Ⅰ)求集合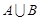 ,
,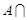
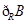 ;
;
(Ⅱ)若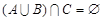 ,求实数
,求实数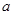 的取值范围.
的取值范围.
已知函数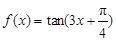
(Ⅰ)求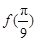 的值;
的值;
(Ⅱ)若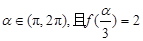 ,求
,求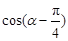 的值.
的值.
通常情况下,同一地区一天的温度随时间变化的曲线接近于函数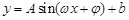 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为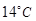 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下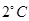 .
.
(Ⅰ)请推理荆门地区该时段的温度函数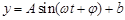
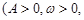
 的表达式;
的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于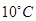 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?
已知向量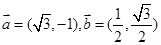
(Ⅰ)求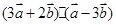 的值;
的值;
(Ⅱ)若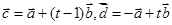 ,且
,且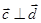 ,求实数t的值.
,求实数t的值.
已知函数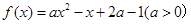
(Ⅰ)设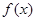 在区间
在区间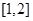 的最小值为
的最小值为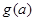 ,求
,求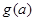 的表达式;
的表达式;
(Ⅱ)设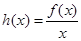 ,若函数
,若函数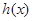 在区间
在区间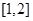 上是增函数,求实数
上是增函数,求实数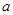 的取值范围。
的取值范围。