抛物线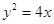 的焦点是
的焦点是
A.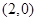 |
B.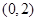 |
C.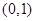 |
D.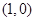 |
命题“如果 都是奇数,则
都是奇数,则 必为奇数”的逆否命题是
必为奇数”的逆否命题是
A.如果 是奇数,则 是奇数,则 都是奇数 都是奇数 |
B.如果 不是奇数,则 不是奇数,则 不都是奇数 不都是奇数 |
C.如果 都是奇数,则 都是奇数,则 不是奇数 不是奇数 |
D.如果 不都是奇数,则 不都是奇数,则 不是奇数 不是奇数 |
已知命题
 ,命题
,命题
 .则命题
.则命题 是命题
是命题 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知向量 ,
, ,且
,且 与
与 互相垂直,则
互相垂直,则 的值是
的值是
A. |
B. |
C. |
D. |
数列 是等差数列,
是等差数列, ,
, ,则
,则
A. |
B. |
C. |
D. |
 中,
中, ,
, ,则
,则
A. |
B. |
C. |
D. |
数列 的通项公式
的通项公式 ,则数列
,则数列 的前10项和为
的前10项和为
A. |
B. |
C. |
D. |
已知椭圆的长轴长是短轴长的 倍,则椭圆的离心率等于
倍,则椭圆的离心率等于
A. |
B. |
C. |
D. |
等差数列 中,若
中,若 ,则该数列前2013项的和为
,则该数列前2013项的和为
A. |
B. |
C. |
D. |
已知 且
且 ,则
,则
| A.有最大值2 | B.有最大值4 | C.有最小值3 | D.等于4 |
数列 为等比数列,
为等比数列, 为其前
为其前 项和,已知
项和,已知 ,则公比
,则公比
A. |
B. |
C. 或 或 |
D. 或 或 |
数列 的通项公式为
的通项公式为 ,若其图像上存在点
,若其图像上存在点 在可行域
在可行域 内,则
内,则 的取值范围为
的取值范围为
A. |
B. |
C. |
D. |
已知 三个数成等比数列,则公比
三个数成等比数列,则公比 _______________.
_______________.
已知正数 满足
满足 ,则
,则 的最小值为_____________.
的最小值为_____________.
椭圆的离心率等于 ,且与双曲线
,且与双曲线 有相同的焦距,则椭圆的标准方程为________________________.
有相同的焦距,则椭圆的标准方程为________________________.
下列四个命题:
①若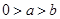 ,则
,则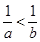 ;
;
②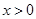 ,
, 的最小值为
的最小值为 ;
;
③椭圆 比椭圆
比椭圆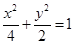 更接近于圆;
更接近于圆;
④设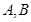 为平面内两个定点,若有
为平面内两个定点,若有 ,则动点
,则动点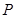 的轨迹是椭圆;
的轨迹是椭圆;
其中真命题的序号为________________.(写出所有真命题的序号)
(本小题满分12分)
已知 分别为
分别为 三个内角
三个内角 的对边,且
的对边,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, ,求
,求 的面积.
的面积.
本小题满分12分)
给定两个命题,  :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :
: .如果
.如果 ∨
∨ 为真命题,
为真命题, ∧
∧ 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)
抛物线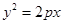 的焦点与双曲线
的焦点与双曲线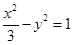 的右焦点重合.
的右焦点重合.
(Ⅰ)求抛物线的方程;
(Ⅱ)求抛物线的准线与双曲线的渐近线围成的三角形的面积.
(本小题满分12分)数列 的前
的前 项和
项和 ,
,
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 求数列
求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
四棱锥 ,面
,面 ⊥面
⊥面 .侧面
.侧面 是以
是以 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 为直角梯形,
为直角梯形, ,
, ∥
∥ ,
, ⊥
⊥ ,
, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证 ⊥
⊥ ;
;
(Ⅱ)求二面角 的正弦值.
的正弦值.
(本小题满分14分)
已知椭圆中心在原点,焦点在x轴上,离心率 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知直线 与椭圆相交于
与椭圆相交于 两点,且坐标原点
两点,且坐标原点 到直线
到直线 的距离为
的距离为 ,
, 的大小是否为定值?若是求出该定值,不是说明理由.
的大小是否为定值?若是求出该定值,不是说明理由.