如图所示, 是全集,
是全集, 是
是 的子集,则阴影部分所表示的集合为
的子集,则阴影部分所表示的集合为
A. |
B. |
C. |
D. |
如果角 的终边经过点
的终边经过点 ,则
,则
A. |
B. |
C. |
D. |
已知向量 ,
, ,若
,若 ,则实数x的值为
,则实数x的值为
| A.1 | B. |
C. |
D. |
如图在四边形 中,设
中,设 ,
, ,
, ,则
,则

A. |
B. |
C. |
D. |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象
的图象
A.向左平移 个单位长度 个单位长度 |
B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
已知 是指数函数,
是指数函数, ,
, 是幂函数,它们的图象如右图所示,则
是幂函数,它们的图象如右图所示,则 的大小关系为
的大小关系为 
A. |
B. |
C. |
D. |
若 则
则 的值是
的值是
A. |
B. |
C. |
D. |
函数 的递增区间是
的递增区间是
A. |
B. |
C. |
D. |
已知 是函数
是函数 的两个零点,则
的两个零点,则
A. |
B. |
C. |
D. |
函数 的图象为如图所示的折线段
的图象为如图所示的折线段 ,其中点
,其中点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .定义函数
.定义函数 ,则函数
,则函数 的最大值为
的最大值为
A. |
B. |
C. |
D. |
设扇形的弧长为 ,半径为8,则该扇形的面积为 .
,半径为8,则该扇形的面积为 .
若向量 ,
, 满足
满足 ,且
,且 与
与 的夹角为
的夹角为 ,则
,则 .
.
 的值为 .
的值为 .
已知函数
 一个周期的图象如图所示.则函数
一个周期的图象如图所示.则函数 的表达式为 .
的表达式为 .
设函数 的零点为
的零点为 ,则不等式
,则不等式 的最大整数解是 .
的最大整数解是 .
已知正方形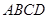 的边长为
的边长为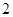 ,
,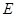 是
是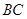 的中点,则
的中点,则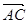 ·
·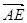 = .
= .
关于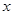 的方程
的方程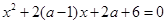 至少有一个正根,则实数
至少有一个正根,则实数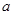 的取值范围为 .
的取值范围为 .
计算: ;
;
解方程: .
.
设向量 ,
, .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求实数
,求实数 的值.
的值.
已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,且
,且 ,求
,求 的值.
的值.
已知 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)直接写出 的单调区间(不需给出演算步骤);
的单调区间(不需给出演算步骤);
(Ⅲ)求不等式 解集.
解集.
已知 ,
, . 记
. 记 (其中
(其中 都为常数,且
都为常数,且 ).
).
(Ⅰ)若 ,
, ,求
,求 的最大值及此时的
的最大值及此时的 值;
值;
(Ⅱ)若 ,①证明:
,①证明: 的最大值是
的最大值是 ;②证明:
;②证明: .
.