下列图案既是中心对称图形，又是轴对称图形的是（ ）
在实数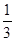
，
，
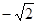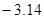，0，
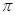中，无理数有 （ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
在下列各式中，正确的是（ ）
A． =±6 |
B． |
C． =0.1 |
D． |
若点A的坐标
满足条件
，则点A在 （ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
正方形具有而菱形不一定具有的性质是（ ）
| A．对角线相等 | B．对角线互相垂直 |
| C．对角线互相平分 | D．对角线平分一组对角 |
已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
| A．当AB=BC时，它是菱形 | B．当AC=BD时，它是正方形 |
| C．当AC⊥BD时，它是菱形 | D．当∠ABC=900时，它是矩形 |
顺次连接四边形四边中点所组成的四边形是 （ ）
| A．矩形 | B．菱形 | C．正方形 | D．平行四边形 |
“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟先到达终点。用s1，s2分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事相吻合的是 （ ）
球的体积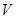
与球的半径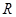
之间的函数关系式：=
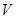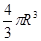，常量是 ，变量是 。
用科学记数法表示：0.000077≈___ ____(保留1个有效数字)
等腰三角形的一个外角为100°，则顶角的度数是 ．
梯形的中位线长为3，高为2，则该梯形的面积为 .
已知点P的坐标是（4，-6），则这个点到x轴的距离是 .
菱形ABCD中，若对角线长AC＝8cm，BD=6cm，则边长AB＝ cm..
若
的值在两个整数a与a+1之间，则a= .
已知一次函数
+3，则
= .
已知点A（a，2a－3）在一次函数y=x+1的图象上，则a= .
如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，当两条纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是 .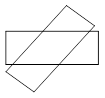
求下列各式中的x：（1）
；（2）
计算：（1）
；（2）
已知y–3与x成正比例，当x=1时y=2.
（1）写出y与x之间的函数关系式
（2）求x=–1时，y的值
在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别相交点E、F.四边形AFCE是菱形吗？为什么？ 
如图，在△ABC中，A（−2，3），B（−3，1），C（−1，2）．
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）将△ABC绕原点O旋转180°，画出旋转后的△A2B2C2；
（3）若P（m，n）为AB边上任一点，写出△A2B2C2中与P点对应的点坐标.
如图，已知在△ABC中，∠ACB=90°，点D、E、F分别是AC、AB、BC的中点，
试说明：CE=DF.
如图，AB两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车从A地出发驶往B地，图中PQR和线段MN，分别表示甲和乙所行驶的路程S与该日下午时间t之间的关系，试根据图形回答：
（1）甲出发几小时，乙才开始出发？
（2）乙行驶多少分钟赶上甲，这时两人离B地还有多少千米？
（3）甲从下午2时到5时的速度是多少？
（4）乙行驶的速度是多少？
平行四边形两个顶点坐标分别为（-3，0），（1，0），第3个顶点在y轴上，且与x轴的距离为3个单位长度.求第4个顶点的坐标.
已知：如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2＋CD2＝2AB2．
（1）求证：AB＝BC；
（2）当BE⊥AD于E时，试证明：BE＝AE＋CD．