已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
在给定的映射 :
: 的条件下,象3的原象是( )
的条件下,象3的原象是( )
| A.8 | B.2或-2 | C.4 | D.-4 |
函数 的值域是( )
的值域是( )
A. |
B. |
C. |
D. |
若函数 的定义域是
的定义域是 ,则函数
,则函数 的定义域是 ( )
的定义域是 ( )
A B.
B.  C.
C.  D.
D. 
设 ,则在下列区间中使函数
,则在下列区间中使函数 有零点的区间是( )
有零点的区间是( )
A. |
B. |
C. |
D. |
已知 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若函数 的定义域为
的定义域为 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
A. |
B. |
C. |
D. |
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. |
B. |
C. |
D. |
下面有四个结论:①偶函数的图像一定与 轴相交。②奇函数的图像不一定过原点。③偶函数若在
轴相交。②奇函数的图像不一定过原点。③偶函数若在 上是减函数,则在
上是减函数,则在 上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知定义域为 的偶函数
的偶函数 在
在 上是减函数,且
上是减函数,且 ,则不等式
,则不等式 ( )
( )
A. |
B. |
C. |
D. |
已知函数 是奇函数,则
是奇函数,则 的值为( )
的值为( )
| A.2013 | B.2012 | C.2011 | D.2010 |
已知函数 是
是 上的增函数,那么实数
上的增函数,那么实数 的范围( )
的范围( )
A. |
B. |
C. |
D. |
设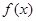 是定义在
是定义在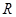 上的奇函数,当
上的奇函数,当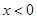 时
时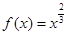 ,则
,则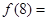 _________.
_________.
函数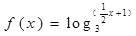 的单调递增区间为_______________.
的单调递增区间为_______________.
二次函数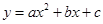 的图像向左平移2个单位,再向上平移3个单位,得到的二次函数为
的图像向左平移2个单位,再向上平移3个单位,得到的二次函数为 ,则
,则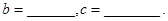
设方程 的根为
的根为 ,方程
,方程 的根为
的根为 ,则
,则
(本小题10分)
已知全集 ,
, 、
、 、
、 ,
,
求:  ;
;  ;
; 
(本小题12分)
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,

(1)求函数 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。
(2)根据图像写出的单调区间和值域。
(本小题12分)
已知函数 ,其中
,其中 。
。
求函数 的最大值和最小值;
的最大值和最小值;
若实数 满足:
满足: 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(本小题12分)已知函数 是幂函数且在
是幂函数且在 上为减函数,函数
上为减函数,函数 在区间
在区间 上的最大值为2,试求实数
上的最大值为2,试求实数 的值。
的值。
(本小题满分12分)
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是 (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
(本小题12分)
已知奇函数 对任意
对任意 ,总有
,总有 ,且当
,且当 时,
时, .
.
(1)求证: 是
是 上的减函数.
上的减函数.
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
(3)若 ,求实数
,求实数 的取值范围。
的取值范围。