已知复数
，则
的共轭复数是
A． |
B． |
C． |
D． |
已知集合
，
，若
，则所有实数
组成的集合是
A． |
B． |
C． |
D． |
下列各小题中，
是
的充要条件的是
（1）
；
（2）
是奇函数；
（3）
；
（4）
或
；
有两个不同的零点.
A． |
B． |
C． |
D． |
已知随机变量
服从正态分布
，且
，则
A． |
B． |
C． |
D． |
方程
表示双曲线，则
的取值范围是
A． |
B． 或 或 |
C． 或 |
D．或 |
一个样本容量为
的样本数据，它们组成一个公差不为
的等差数列
，若
且前
项和
，则此样本的平均数和中位数分别是
A． |
B． |
C． |
D． |
右面的程序框图中，若输出
的值为
，则图中应填上的条件为 
A． |
B． |
C． |
D． |
设函数
，则下列结论正确的是
A． 的图像关于直线 对称 |
B．的图像关于点 对称 |
C．的最小正周期为 ，且在 上为增函数 |
D．把的图像向右平移 个单位，得到一个偶函数的图像 |
设
为平面上四点，
，则
A．点 在线段 上 |
B．点 在线段 上 |
C．点 在线段 上 |
D．四点共线 |
二项式
的展开式的第二项的系数为
，则
的值为
A． |
B． |
C．或 |
D．或 |
在平面直角坐标系
中，圆
的方程为
，若直线
上至少存在一点，使得以该点为圆心，
为半径的圆与圆有公共点，则
的最大值为
A． |
B． |
C． |
D． |
对于正实数
，记
为满足下述条件的函数
构成的集合：
且
，有
.下列结论中正确的是
A．若 ，则 |
B．若且 ，则 |
C．若，则 |
D．若且 ，则 |
设不等式组
表示的平面区域为
，在区域内随机取一个点，则此点到坐标原点的距离大于
的概率是 ．
已知命题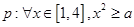
,命题
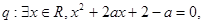若命“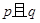
”是真命题,则实数
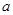的取值范围为 .
如图，已知球
的面上有四点
，
平面
,
,
,则球的体积与表面积的比为 ． 
函数
的零点的个数是 ．
（本小题满分12分）
设
的内角
所对的边分别为
且
.
(Ⅰ)求角
的大小;
(Ⅱ)若
,求的周长
的取值范围.
（本小题满分12分）
某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛，规则如下：两名选手比赛时，每局胜者得
分，负者得
分，比赛进行到有一人比对方多
分或打满
局时结束.假设选手甲与选手乙比赛时，甲每局获胜的概率皆为
，且各局比赛胜负互不影响.
（Ⅰ）求比赛进行
局结束，且乙比甲多得分的概率；
（Ⅱ）设
表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望．
（本小题满分12分）
如图，在多面体
中，平面
∥平面
，
⊥平面，
,
,
∥
．
且
, 
．
（Ⅰ）求证：
平面
;
（Ⅱ）求证：
∥平面
；
（Ⅲ）求二面角
的余弦值．
已知数列
为公差不为
的等差数列，
为前
项和，
和
的等差中项为
，且
．令
数列
的前项和为
．
（Ⅰ）求
及；
（Ⅱ）是否存在正整数
成等比数列？若存在，求出所有的
的值；若不存在，请说明理由．
(本小题满分12分）
设点
到直线
的距离与它到定点
的距离之比为
，并记点
的轨迹为曲线
．
（Ⅰ）求曲线的方程;
（Ⅱ）设
，过点
的直线
与曲线相交于
两点，当线段
的中点落在由四点
构成的四边形内（包括边界）时，求直线斜率的取值范围．
(本小题满分14分）
已知函数
为常数)是实数集
上的奇函数，函数
在区间
上是减函数．
（Ⅰ）求实数
的值；
（Ⅱ）若
在
上恒成立，求实数
的最大值；
（Ⅲ）若关于
的方程
有且只有一个实数根，求
的值．