若集合 ,
, ( )。
( )。
A. |
B. |
C. |
D. |
如图,该程序运行后输出的结果为( )。
| A.36 | B.45 | C.55 | D.56 |
抛物线 的准线方程是( )。
的准线方程是( )。 .
.
 .
.
 .
.
 .
.
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )。
A.4(9+2 ) cm2 ) cm2 |
B. cm2 cm2 |
C. cm2 cm2 |
D. cm cm |
在 中,下列关系式不一定成立的是( )。
中,下列关系式不一定成立的是( )。
A. |
B. |
C. |
D. |
在等差数列中, ,
, ,
, ,则
,则 的值为( )。
的值为( )。
| A.14 | B.15 | C.16 | D.75 |
已知 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题:
①若 ,
, ,
, ,则
,则 或
或 .
.
②若 ,
, ,
, ,则
,则 .
.
③若m
 ,n
,n
 ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
④若 ,
, 且
且 ,
, ,则
,则
其中正确的命题是( )。
| A.①② | B.②④ | C.②③ | D.③④ |
设实数 满足约束条件:
满足约束条件: ,则
,则 的最大值为( )。
的最大值为( )。
A. |
B.68 | C. |
D.32 |
已知圆C: 和点
和点 ,P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
,P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
A. . . |
B. |
C. |
D. |
设 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若点
)的两个焦点, 若点 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。
A. |
B. |
C. |
D.3 |
已知直线
 与抛物线
与抛物线 相交于
相交于 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若 ,则k的值为( )。
,则k的值为( )。
A. |
B. |
C. |
D. |
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设 ,
, ,
, ,则
,则 、
、 、
、 的大小顺序是( )。
的大小顺序是( )。
A. |
B. |
C. |
D. |
已知平行六面体 ,底面
,底面 是正方形,
是正方形, ,则棱
,则棱 和底面所成角为 。
和底面所成角为 。
已知向量 满足则
满足则 ,则
,则 。
。
已知直线 ,
, 平分圆
平分圆 的周长,则
的周长,则 取最小值时,双曲线
取最小值时,双曲线 的离心率为 。
的离心率为 。
在区间 上随机取一个数
上随机取一个数 ,则事件
,则事件 发生的概率为 。
发生的概率为 。
已知命题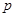 :
: 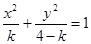 表示焦点在
表示焦点在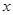 轴上的椭圆,命题
轴上的椭圆,命题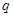 :
: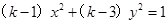 表示双曲线。若
表示双曲线。若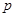 或
或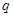 为真,
为真,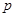 且
且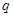 为假,求
为假,求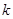 的取值范围。
的取值范围。
若关于 的不等式
的不等式 的解集是
的解集是 ,
, 的定义域是
的定义域是 ,若
,若 ,求实数
,求实数 的取值范围。
的取值范围。
平面直角坐标系中有一个△ABC,角A,B,C所对应的边分别为 ,已知坐标原点与顶点B重合,且
,已知坐标原点与顶点B重合,且 ,
, ,
, =
= ,且∠A为锐角。
,且∠A为锐角。
(1)求角A的大小;
(2)若 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,顶点A
,顶点A ,
, ,求△ABC的面积。
,求△ABC的面积。
如图所示在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形。
(1)求PC和平面ABCD所成角的大小;
(2)求二面角B─AC─P的大小。
已知函数 =
= ,数列
,数列 满足
满足 ,
, 。
。
(1)求数列 的通项公式;
的通项公式;
(2)令 -
- +
+ -
- +…+
+…+ -
- 求
求 ;
;
(3)令 =
= (
( ,
, ,
,
 +
+ +
+ +┅
+┅ ,若
,若 <
< 对一切
对一切 都成立,求最小的正整数
都成立,求最小的正整数 。
。
已知椭圆 的中心为坐标原点
的中心为坐标原点 ,一个长轴端点为
,一个长轴端点为 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于不同的两点
交于不同的两点 ,且
,且 。
。
(1)求椭圆 的方程;
的方程;
(2)求实数 的取值范围。
的取值范围。