命题p:“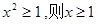 ”的否定
”的否定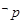 是 .
是 .
已知椭圆的长轴长是短轴长的 倍,则椭圆的离心率等于 .
倍,则椭圆的离心率等于 .
已知 ,则“
,则“ ”是“
”是“ ”的 条件.
”的 条件.
已知a,b,c分别是△ABC的三个内角A,B,C的对边长,若 ,则A等于 .
,则A等于 .
已知等比数列 的前三项依次为
的前三项依次为 ,
, ,
, ,则
,则 .
.
若双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则此双曲线的离心率为 。
,则此双曲线的离心率为 。
抛物线 上一点
上一点 到焦点的距离为3,则点
到焦点的距离为3,则点 的横坐标是 .
的横坐标是 .
若x,y满足约束条件: 则
则 的最小值为 .
的最小值为 .
对于任意实数x,不等式 恒成立,则实数a的取值范围是 。
恒成立,则实数a的取值范围是 。
点P是椭圆 上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
若曲线 :
: 上所有的点均在第二象限内,则
上所有的点均在第二象限内,则 的取值范围为 。
的取值范围为 。
一次函数 的图象同时经过第一、三、四象限的一个充分不必要条件是 。
的图象同时经过第一、三、四象限的一个充分不必要条件是 。
在括号里填上和为1的两个正数,使 的值最小, 则这两个正数的积等于 .
的值最小, 则这两个正数的积等于 .
设 是
是 内一点,
内一点, ,定义
,定义 ,其中
,其中 分别是
分别是 的面积,若
的面积,若 ,则
,则 的最小值是 。
的最小值是 。
在 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是 、b、c,已知
、b、c,已知 ,且
,且 的夹角为
的夹角为 。
。
(Ⅰ)求内角C的大小;
(Ⅱ)已知 ,三角形的面积
,三角形的面积 ,求
,求 的值。
的值。
已知p: ≤2; q:
≤2; q: ≤0(m>0),若
≤0(m>0),若 是
是 的充分而不必要条件,求实数m的取值范围.
的充分而不必要条件,求实数m的取值范围.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.
已知曲线 过点P(1,3),且在点P处的切线
过点P(1,3),且在点P处的切线
恰好与直线 垂直.求 (Ⅰ) 常数
垂直.求 (Ⅰ) 常数 的值; (Ⅱ)
的值; (Ⅱ) 的单调区间.
的单调区间.
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
已知数列 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为 的等差数列;
的等差数列; 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(Ⅰ)若 = 30,求
= 30,求 ;
;
(Ⅱ)试写出a30关于 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得 是公差为
是公差为 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出 关于
关于 的关系式(
的关系式( N
N );
);
(Ⅳ)在(Ⅲ)条件下,且 ,试用
,试用 表示此数列的前100项和
表示此数列的前100项和