下面是关于复数 的四个命题( )
的四个命题( ) :
: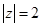 ;
;  :
: ;
;  :
: 的共轭复数为
的共轭复数为 ;
;  :
: 的虚部为
的虚部为
其中的真命题为
A. , , |
B. , , |
C. , , |
D. , , |
设 ,则“函数
,则“函数 在R上是减函数”是“函数
在R上是减函数”是“函数 在R上为减函数”的( )
在R上为减函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要 |
已知直线 与曲线
与曲线 在点
在点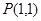 处的切线互相垂直,则
处的切线互相垂直,则 为( )
为( )
A. |
B.  |
C. |
D. |
已知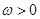 ,函数
,函数 在
在 上单调递减,则
上单调递减,则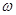 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若函数 (
( )是奇函数 ,则
)是奇函数 ,则 ( )
( )
A.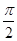 |
B. |
C. |
D. |
平面向量 与
与 的夹角为
的夹角为 ,若
,若 ,
, ,则
,则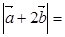 ( )
( )
A. |
B. |
C.4 | D.12 |
当 时,
时, ,那么
,那么 的取值范围是( )
的取值范围是( )
A. |
B. |
C.(1, 4) | D.(2, 4 ) |
函数
 的零点的个数( )
的零点的个数( )
| A.0 | B.1 | C.2 | D.3 |
已知函数 在
在 单调递减,则
单调递减,则 的取值范围( )
的取值范围( )
A. |
B. |
C. |
D. |
在实数的原有运算法则中,我们补充定义新运算“ ”如下:当
”如下:当 时,
时, ;当
;当 时,
时, 。则函数
。则函数 有( )(“·”和“-”仍为通常的乘法和减法)
有( )(“·”和“-”仍为通常的乘法和减法)
A.最大值为 ,无最小值 ,无最小值 |
B.最大值为 ,最小值为1 ,最小值为1 |
| C.无最大值,无最小值 | D.无最大值,最小值为1 |
已知偶函数 在区间
在区间 上是增函数,且满足
上是增函数,且满足 ,下列判断中错误的是( )
,下列判断中错误的是( )
A.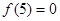 |
B.函数 在 在 上单调递减 上单调递减 |
C.函数 的图像关于直线 的图像关于直线  对称 对称 |
D.函数 的周期是 的周期是 |
若 且
且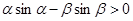 .则下列结论正确的是( )
.则下列结论正确的是( )
A. |
B. |
C. |
D. |
把函数y=sin(2x- )的图象向左平移
)的图象向左平移 个单位后,所得函数图象的一条对称轴为 .
个单位后,所得函数图象的一条对称轴为 .
已知函数 对任意的
对任意的 恒成立,则
恒成立,则 ________.
________.
对于正项数列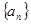 ,定义
,定义 ,若
,若 则数列
则数列 的通项公式为 .
的通项公式为 .
设方程 的解为
的解为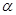 ,方程
,方程 的解为
的解为 ,则
,则 的值为 .
的值为 .
设命题 :函数
:函数 =
= 是
是 上的减函数,命题
上的减函数,命题 :函数
:函数 的定义域为
的定义域为 ,若“
,若“ 且
且 ”为假命题,“
”为假命题,“ 或
或 ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围.
已知函数
 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
.
(1)求值;
(2)若 ,且有且仅有一个实根,求实数
,且有且仅有一个实根,求实数 的值.
的值.
已知数列 中,
中, .
.
(1)写出 的值(只写结果)并求出数列
的值(只写结果)并求出数列 的通项公式;
的通项公式;
(2)设 , 若对任意的正整数
, 若对任意的正整数 ,当
,当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校男生的人数;
(2)估计该校学生身高在170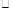 185cm之间的概率;
185cm之间的概率;
定义在R上的单调函数 满足
满足 且对任意
且对任意 都有
都有 .
.
(1)求证 为奇函数;
为奇函数;
(2)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.