x与3的和不小于－6，用不等式表示为 .
若a<b，则：a－3____b－3；
（填“﹥、﹤或=”号）.
当x 时，分式
有意义，当x= ,分式
的值是0.
不等式组
的非负整数解是______________.
化简：
＝ ； 
＝ .
若分式方程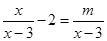
有增根，则
的值为_____________．
已知x=3是方程
的解，那么不等式
的解集是 .
已知
，则分式
的值为 .
若不等式组
的解集是x>3,则m的取值范围是 .
解方程
时，若设
，则方程可化为 ．
如果-1＜x＜0，则下列不等式成立的是（ ）
A．x ＞ ＞x |
B．＞x＞x |
C．x＞＞x |
D．x＞x＞ |
下列代数式
2a-5b中，分式的个数是 （ ）
| A．1 | B．2 | C．3 | D．4 |
下列分式中，最简分式是（ ）
A． |
B． |
C． |
D． |
下列运算中，错误的是（ ）
A． |
B． = - |
C． |
D． = -1 |
分式
中x、y的值都扩大为原来的4倍，则分式的值 （ ）
| A．扩大为原来的4倍 | B．不变 | C．缩小为原来的 倍 |
D．无法确定 |
已知点M（m﹣1， 2m﹣1）关于y轴的对称点在第一象限，则m的取值范围在数轴上表示正确的是（ ）
A． |
B． |
C． |
D． |
观察下列图象，可以得到不等式组
的解集是 （ ）
A． |
B． |
C． |
D． |
关于x的不等式组
只有6个整数解，则a的取值范围是（ ）
A．－ ≤a≤－4 |
B．－＜a≤－4 |
| C．－≤a＜－4 |
D．－＜a＜－4＝＝ |
解不等式：
解不等式组
并在数轴上把解集表示出来
化简：
化简：
再选择一个你喜欢的值代入求值
解方程：
解方程：
已知关于x、y的方程组
的解是负数．求k的取值范围.
某中学为落实市教育局提出的“全员育人，创办特色学校”的会议精神，决心打造“书香校园”，计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．
（1）符合题意的组建方案有几种？请你帮学校设计出来；
（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570
元，试说明（1）中哪种方案费用最低，最低费用是多少元？
我们知道，分式和分数有着很多的相似点.小学里，把分子比分母小的分数叫做真分数.类似的，我们把分子的次数小于分母的次数的分式称为真分式，反之，称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式，如 
.
(1)下列分式中，属于真分式的是（ ）
A． |
B． |
C． |
D． |
(2)将假分式
，化成整式和真分式的和的形式.
某楼盘一楼是车库（暂不销售），二楼至二十三楼均为商品房（对外销售）.商品房售价方案如下：第八层售价为3000元/米2，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案：
方案一：购买者先交纳首付金额（商品房总价的30％），再办理分期付款（即贷款）.
方案二：购买者若一次付清所有房款，则享受8％的优惠，并免收五年物业管理费（已知每月物业管理费为a元）
（1）请写出每平方米售价
（元/米2）与楼层
（2≤≤23，是正整数）之
间的函数解析式；
（2）小张已筹到120000元，若用方案一购房，他可以购买哪些楼层的商品房呢？
（3）有人建议老王使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9％的优惠划算.你认为老王的说法一定正确吗？请用具体的数据阐明你的看法.