设a>0,b>0,且a2 + b2 = a + b,则a + b的最大值是( )
A. |
B. |
C.2 | D.1 |
已知 ,且
,且
求证:
关于x的不等式|x-2|+|x-a|≥a在R上恒成立,求实数a的取值范围.
(不等式选讲选做题)若 的最小值为3,
的最小值为3,
则实数 的值是________.
的值是________.
设a、b、c均为实数,求证: +
+ +
+ ≥
≥ +
+ +
+ .
.
若不等式 >mx+
>mx+ 的解集为4<x<n,则m、n的值分别是
的解集为4<x<n,则m、n的值分别是
A.m= ,n="36" ,n="36" |
B.m= ,n=32 ,n=32 |
C.m= ,n="28" ,n="28" |
D.m= ,n=24 ,n=24 |
本题考查同解不等式的意义,方程与不等式的关系.
设实系数一元二次方程 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间 内,另一根在区间
内,另一根在区间 内,则
内,则 的取值范围是 。
的取值范围是 。
不等式 对一切
对一切 均成立,则实数
均成立,则实数 的取值范围是_______________
的取值范围是_______________
设 ,
, ,则
,则 三数 ( )
三数 ( )
| A.至少有一个不小于2 | B.都大于2 |
| C.至少有一个不大于2 | D.都小于2 |
不等式 与
与 能同时成立的充要条件是 ( )
能同时成立的充要条件是 ( )
A  B
B 
C  D
D 
使不等式 成立的一个充分不必要条件是
成立的一个充分不必要条件是
设函数 ,不等式
,不等式 的解集为(-1,2)
的解集为(-1,2)
(1)求 的值;
的值;
(2)解不等式 .
.
函数 的最小值为( )
的最小值为( )
| A.10 | B.9 | C.6 | D.4 |
已知
(1)若p > 1时,解关于x的不等式 ;
;
(2)若 对
对 时恒成立,求p的范围.
时恒成立,求p的范围.
不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
若a是1+2b与1-2b的等比中项,则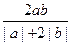 的最大值为( )
的最大值为( )
A.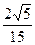 |
B.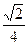 |
C. |
D.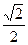 |
设函数
(1)当 时,求函数
时,求函数 的定义域;
的定义域;
(2)若函数 的定义域为R,试求
的定义域为R,试求 的取值范围。
的取值范围。
若 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. |
B. |
C. |
D. |